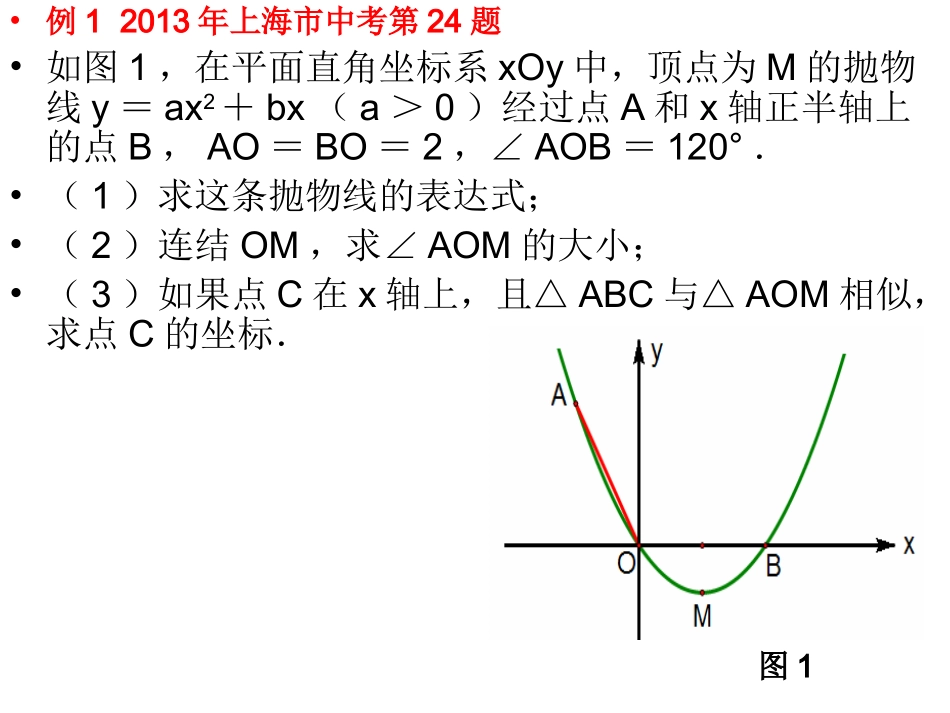
2014年中考数学压轴题第一部分函数图象中点的存在性问题•1.1因动点产生的相似三角形问题•例12013年上海市中考第24题•如图1,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,AO=BO=2,∠AOB=120°.•(1)求这条抛物线的表达式;•(2)连结OM,求∠AOM的大小;•(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.图1•思路点拨•1.第(2)题把求∠AOM的大小,转化为求∠BOM的大小.•2.因为∠BOM=∠ABO=30°,因此点C在点B的右侧时,恰好有∠ABC=∠AOM.•3.根据夹角相等对应边成比例,分两种情况讨论△ABC与△AOM相似.•(1)如图2,过点A作AHy⊥轴,垂足为H.•在RtAOH△中,AO=2,∠AOH=30°,•所以AH=1,OH=.所以A(-1,)•因为抛物线与x轴交于O、B(2,0)两点,•设y=ax(x-2),代入点A(-1,)可得a=.•所以抛物线的表达式为33333xxxxy332233233图2•(2)由•得抛物线的顶点M的坐标为(1,).所以•tanBOM∠=•所以∠BOM=30°.所以∠AOM=150°.xxxxy3322332333333考点伸展•在本题情境下,如果△ABC与△BOM相似,求点C的坐标如图5,因为△BOM是30°底角的等腰三角形,∠ABO=30°,因此△ABC也是底角为30°的等腰三角形,AB=AC,根据对称性,点C的坐标为(-4,0).图5例22012年苏州市中考第29题图1图2图3考点伸展第(3)题的思路是,A、C、O三点是确定的,B是而∠QOA与∠QOC是互余的,那么我们自然想到三个三角形都是直角三角形的情况.这样,先根据△QOA与△QOC相似把点Q的位置确定下来,再根据两直角边对应成比例确定点B的位置.如图中,圆与直线x=1的另一个交点会不会是符合题意的点Q呢?如果符合题意的话,那么点B的位置距离点A很近,这与OB=4OC矛盾.例32012年黄冈市中考模拟第25题图1图2图3图4例42010年义乌市中考第24题•如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3)•(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;•解:抛物线的对称轴为直线,•解析式为,•顶点为M(1,).图181•如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).•(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B1的坐标分别为(x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;图1图2图1图2•如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.(3)设直线AB与PQ交于点G,直线AB与抛物线的对称轴交于点E,直线PQ与x图3图4例52009年临沂市中考第26题•如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.•(1)求此抛物线的解析式•如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.•(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由图3图4•如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.•(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标图5图61.2因动点产生的等腰三角形问题例例1201312013年上海市虹口区中考模拟第年上海市虹口区中考模拟第2525题题•如图1,在RtABC△中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DEBC⊥交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°•(1)求ED、EC的长;•(2)若BP=2,求CQ的长;•(3)记线段PQ与线段DE的交点为F,...