二次函数y=a（x-h)2+k的图象（1）VIP免费

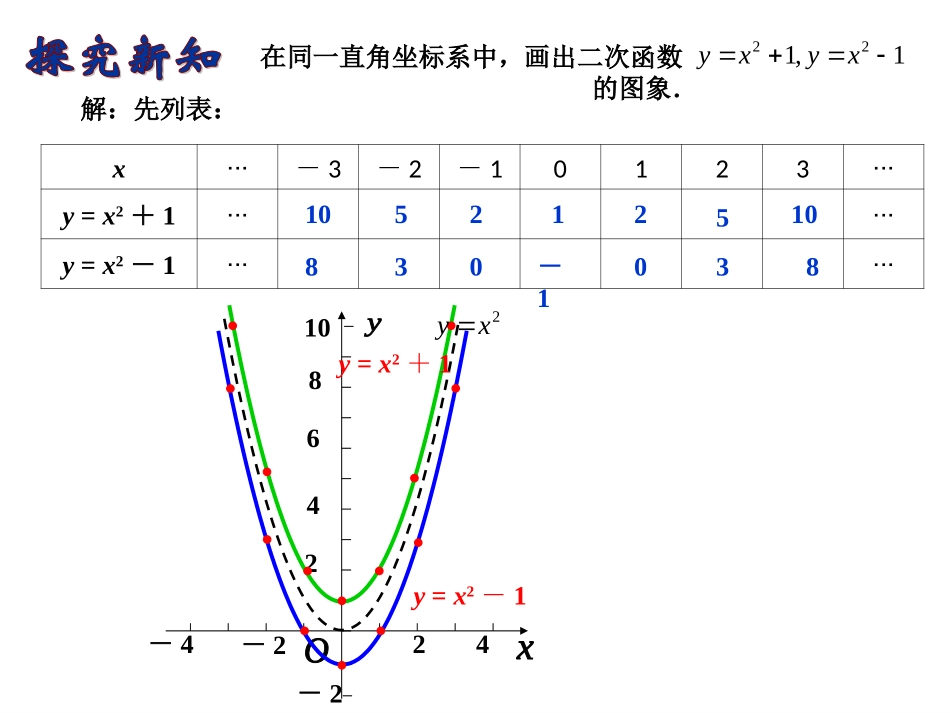
第二十六章二次函数zxx```k二次函数二次函数yy==aa（（xx--hh))22++kk的图象的图象（（11））二次函数y=ax2的图象是一条__________,当a＞0时,抛物线y=ax2的开口________,当a＜0时,抛物线y=ax2的开口________,抛物线y=ax2的顶点是________________,对称轴是_____________________.抛物线向上向下原点(0,0)y轴(即直线x=0)4－22246－4810－2在同一直角坐标系中，画出二次函数的图象．解：先列表：x···－3－2－10123···y=x2＋1······y=x2－1······1,122xyxy105212510830－1038y=x2＋1y=x2－12xy（1）抛物线的开口方向、对称轴、顶点各是什么？（2）抛物线与抛物线有什么关系？1,122xyxy1,122xyxy2xy开口方向都向上，对称轴为y轴，y=x2＋1的顶点坐标是（0，1），y=x2－1的顶点坐标是（0，－1）.4－22246－4810－2y=x2＋1y=x2－12xy4－22246－4810－2y=x2＋1y=x2－12xyy＝ax2+ka>0a<0图象开口方向对称性顶点增减性二次函数y=ax2+k的性质二次函数y=ax2+k的性质开口向上开口向下关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减在对称轴右侧递增在对称轴左侧递增在对称轴右侧递减(0,k)把抛物线y=2x2向上平移5个单位，会得到哪条抛物线？向下平移3.4个单位呢？22yx－222464－48－2－4522xy4.322xy二次函数y=ax2+k的图象可以由二次函数y=ax2的图象平移得到.如果k>0,将y=ax2的图象向上平移k个单位可以得到y=ax2+k的图象；如果k<0,将y=ax2的图象向下平移∣k∣个单位可以得到y=ax2+k的图象.平移前后图象的开口方向、对称轴不变，对称轴左右两侧的增减性不变，顶点的横坐标不变，纵坐标随k变化.Zx```x```k抛物线开口方向对称轴顶点坐标y=2x2+5y=-3x2-2y=-x2+3向上y轴(0,5)y轴y轴向下向下(0,-2)(0,3)1.填写下列表格：2.抛物线y=−2x2+3的顶点坐标是,对称轴是______________，在___________侧，y随着x的增大而增大；在侧，y随着x的增大而减小，当x=______时，函数y的值最（大、小）是,它是由抛物线y=−2x2沿______向_____平移_______个单位长度得到的.上y轴（直线x=0）(0,3)y轴3大3y轴左y轴右01.已知抛物线y=ax2+c经过点（-3，2）、（0，-1），求该抛物线的解析式.2.若点A（1，y1）、B（2，y2）、C（-6，y3）是二次函数y＝－x2＋2图象上的三点，则y1、y2、y3的大小关系是（）A．y1>y2>y3B．y1>y3>y2C．y2>y1>y3D．y2>y3>y1A1.已知抛物线的对称轴是y轴，顶点纵坐标是-3，且经过点（1，2），求该抛物线的解析式.Z```xx```k2.如图，已知⊙P的半径为1，圆心P在抛物线y＝x2－1上运动，当⊙P与x轴相切时，圆心P的坐标为___________________________.(0,-1)(,1)2(,1)23.在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致是如图中的（）xyoAxyoCxyoBxoyDBxyoAxyoB2.抛物线y=ax2+k与y=ax2的联系和区别.小结1.抛物线y=ax2+k的性质.y＝ax2+ka>0a<0图象开口方向对称性顶点增减性二次函数y=ax2+k的性质二次函数y=ax2+k的性质开口向上开口向下关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减在对称轴右侧递增在对称轴左侧递增在对称轴右侧递减(0,k)二次函数y=ax2+k的图象可以由二次函数y=ax2的图象平移得到.如果k>0,将y=ax2的图象向上平移k个单位可以得到y=ax2+k的图象；如果k<0,将y=ax2的图象向下平移∣k∣个单位可以得到y=ax2+k的图象.平移前后图象的开口方向、对称轴不变，对称轴左右两侧的增减性不变，顶点的横坐标不变，纵坐标随k变化.二次函数y=ax2+k与y=ax2的联系二次函数y=ax2+k与y=ax2的联系当堂检测1.2.3.下2432xy41布置作业1.必做题：教材习题26.1第5（1）、7、8题.2.选做题：如图，抛物线y＝ax2＋c（a＞0）经过梯形ABCD的四个顶点，梯形的底AD在x轴上，其中A（－2,0），B（－1,－3）．（1）求抛物线的解析式；（2）点M为y轴上任意一点，当点M到A、B两点的距离之和为最小时，求此时点M的坐标.