高中数学必修1课件_131单调性与最大(小)值1VIP免费

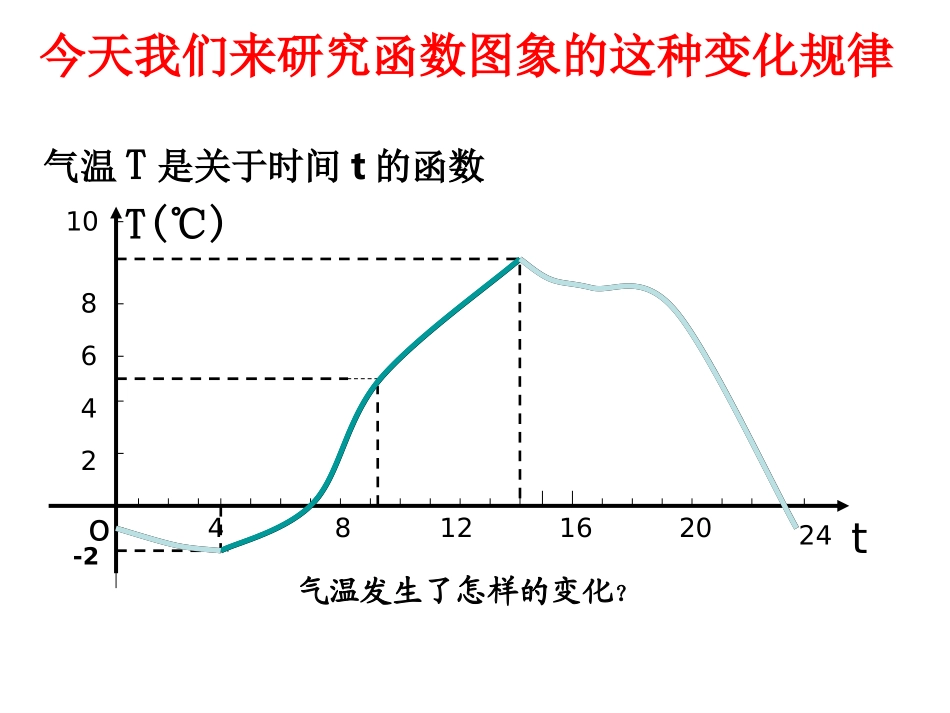
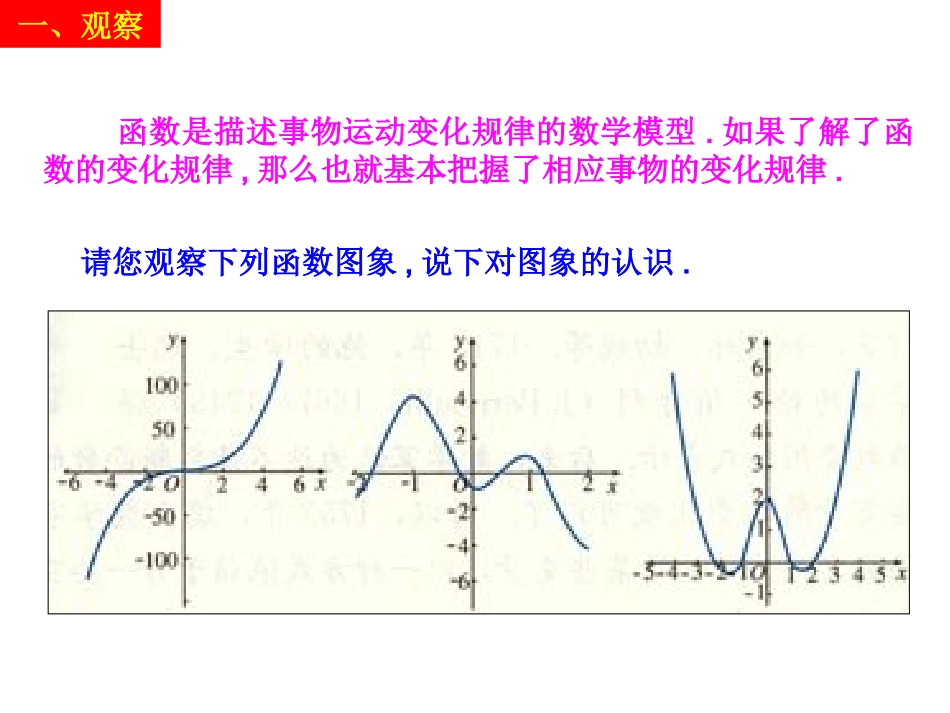
T(℃)气温T是关于时间t的函数4812162024to-2248610气温发生了怎样的变化？今天我们来研究函数图象的这种变化规律函数是描述事物运动变化规律的数学模型.如果了解了函数的变化规律,那么也就基本把握了相应事物的变化规律.请您观察下列函数图象,说下对图象的认识.一、观察观察函数f(x)=x与f(x)=x2的图象是怎样变化的,它们有怎样的升降规律?不同的函数,其图象的变化趋势可能也不同,同一函数在不同区间上的变化趋势也不一定相同.函数图象的这种变化规律反映了函数的一个重要性质---函数的单调性一、观察()fxx2()fxx函数值随着自变量的增大而增大在某个区间上具有这种性质的函数称这个函数在这个区间上是增函数.二、单调性的定义((),)fxx在上的图象上升(2()0,)fxx在上的图象上升图形语言()1212()(),,xxfxxxf在上任意改变的值都有()1212)0(),,(xxxfxfx在上任意改变的值都有符号语言X1X2F(x1)F(x2)文字语言二、单调性的定义观察在某个区间上具有这种性质的函数称这个函数在这个区间上是减函数..((),0)fxx在上的图象是下降的图形语言()1212)0(),,(xxxfxfx在上任意改变的值都有符号语言函数值随着自变量的增大而减小文字语言三、例题()用定义证明函数增减函数的步骤()12121,,xxDxx设且12(2)()()fxfx判断的符号()223:)(),;)(),;fxfx11结论若f(x则为增函数若f(x则为减函数三、例题(,0)(0,)(),0在上单调递减(0,+)在上单调递减三、例题请您观察下列图象,比较两个函数图象及其值域,您能发现什么?(),.fxx函数的图象没有最低点因此没有最小值()22()0,0,,()(0),()0fxxxRfxffxx函数的图象上有一个最低点也就是说对任意的都有因此函数有最小值,:I设函数的定义域为如果满足()001,()xIfxM存在有(2),()xIfxM对于任意的都有().Mfx是函数的称最小值则四、最大(小)值()22()0,0,,()(0),()0.fxxxRfxffxx函数的图象上有一个最高点也就是说对任意的都有因此函数有最大值,:I设函数的定义域为如果满足()001,()xIfxM存在有(2),()xIfxM对于任意的都有().Mfx是函数的称最大值则请您观察函数图象,说明最大值的含义2()fxx四、最大(小)值四、最大(小)值对于不熟悉的函数,可以先画出图象,观察其单调性,再用定义证明,然后利用单调性求出函数的最值.maxmin2(2)2,(6).5yfyf四、最大(小)值2()22(0)[2,3]52,,.fxaxaxbaab已知函数在上有最大值和最小值求的值2:()(1)2fxaxba解(1)0,()[2,3]afx当时在上是增函数(2)2(3)5ff则4421,029625aabaabab(2)0,()[2,3]afx当时在上是减函数(2)5(3)2ff则4421,359622aabaabab四、最大(小)值1、函数单调性的定义增函数减函数五、小结3、求函数最值的一般方法(1)对于熟悉的正比例函数、反比例函数、一次函数和二次函数等,可以先画出在其定义域的图象求其最值.(2)对于不熟悉的函数可以先画出其图象,观察其单调性,再用定义证明,然后利用单调性求其最值.2、用定义证明函数的单调性()12121,,xxDxx设且12(2)()()fxfx判断的符号()223:)(),;)(),fxfx11结论若f(x则为增函数若f(x则为减函数.五、小结