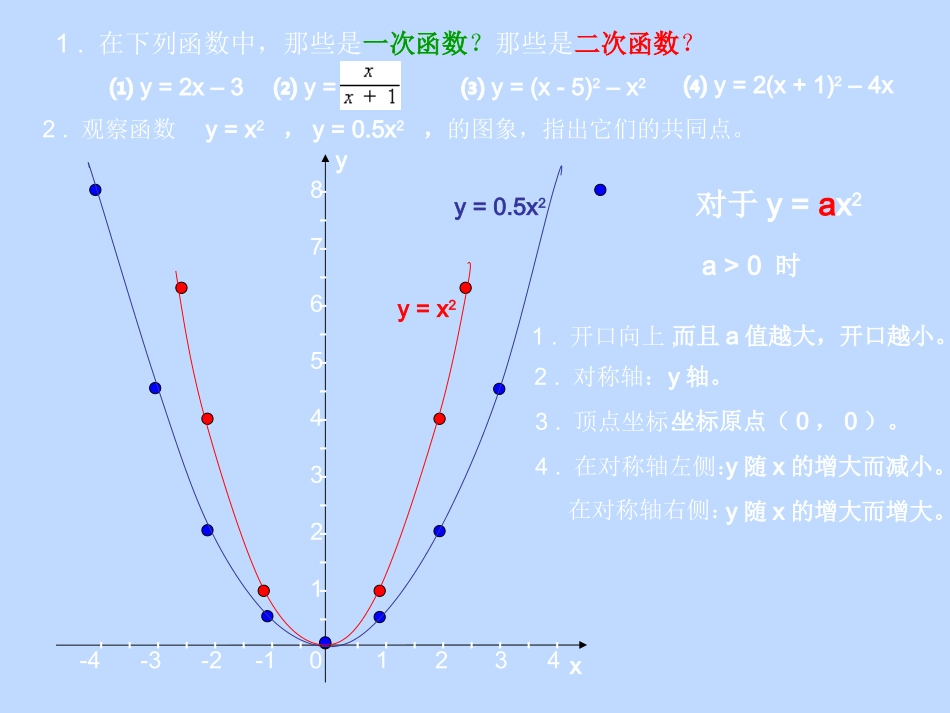
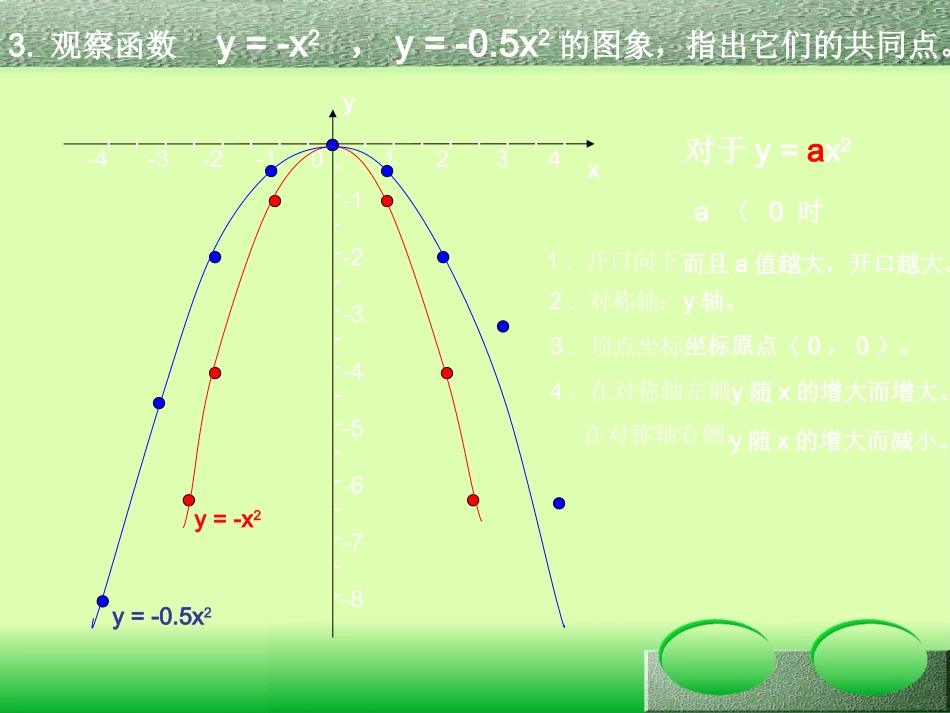
二次函数y=ax2的图象1.在下列函数中,那些是一次函数?那些是二次函数?-----------------4-3-2-101234y=x2y=0.5x2⑴y=2x–3⑶y=(x-5)2–x2⑵y=⑷y=2(x+1)2–4xxy对于y=ax2a>0时1.开口向上,2.对称轴:3.顶点坐标:4.在对称轴左侧:而且a值越大,开口越小。y轴。坐标原点(0,0)。y随x的增大而减小。在对称轴右侧:y随x的增大而增大。----------------876543212.观察函数y=x2,y=0.5x2,的图象,指出它们的共同点。3.观察函数y=-x2,y=-0.5x2的图象,指出它们的共同点。-----------------4-3-2-101234对于y=ax2a〈0时1.开口向下,2.对称轴:3.顶点坐标:4.在对称轴左侧:y轴。坐标原点(0,0)。在对称轴右侧:-----------------1-2-3-4-5-6-7-8yxy=-x2y=-0.5x2y随x的增大而增大。y随x的增大而减小。而且a值越大,开口越大。总结y=ax2的图象性质:xy-----------------4-3-2-101234--------------------987654321-1-2-3-4-5-6-7-8-9y=x2y=0.5x2y=-x2y=-0.5x2对于y=ax2①开口方向:②对称轴:③顶点坐标:④当抛物线开口向上时,在对称轴左侧,y随x增大而减小,在对称轴右侧,y随x增大而增大,这时顶点是最低点。因此,当x=0时,y最小值=0。a>0时,开口向上。a<0时,开口向下。y轴。坐标原点(0,0)。当抛物线开口向下时,在对称轴左侧,y随x增大而增大,在对称轴右侧,y随x增大而减小,这时顶点是最高点。因此,当x=0时,y最大值=0。│a│越大,抛物线的开口越小。向上向下y轴y轴(0,0)(0,0)⒈函数y=x2的图象开口______,对称轴是________,顶点坐标是_________。⒉函数y=-x2的图象开口______,对称轴是________,顶点坐标是_________。⒊函数y=kxk–2k–6是二次函数,当k=_____时,其图象是开口向上;2当k=_____时,其图象是开口向下。⒋从图象上看,函数y=-5x2有最大值或最小值吗?如果有,是最大值还是最小值?这个值是多少?4-2yxy最大值=0已知函数y=ax2(a≠0)与函数y=kx–2的图象相交于A、B两点,其中点A的坐标是(-1,-1)。求:⑴a、k的值;⑵B点的坐标。2解:⑴∵点A在抛物线y=ax2,也在直线y=kx–2上∴-1=a(-1)∴a=-1∴-1=k(-1)-2∴k=-1⑵∵a=-1,k=-1∴得到函数y=-x2;y=-x–2y=-x2x1=-1x1=2∴∴解得y=-x–2y1=-1y2=-4本课小结:这节课我学到了什么?作业:课本P114--------B组1、2题练习册讲解内容:二次函数y=ax2的图象课件制作:杨彦平日期:二零零三年十一月二十日