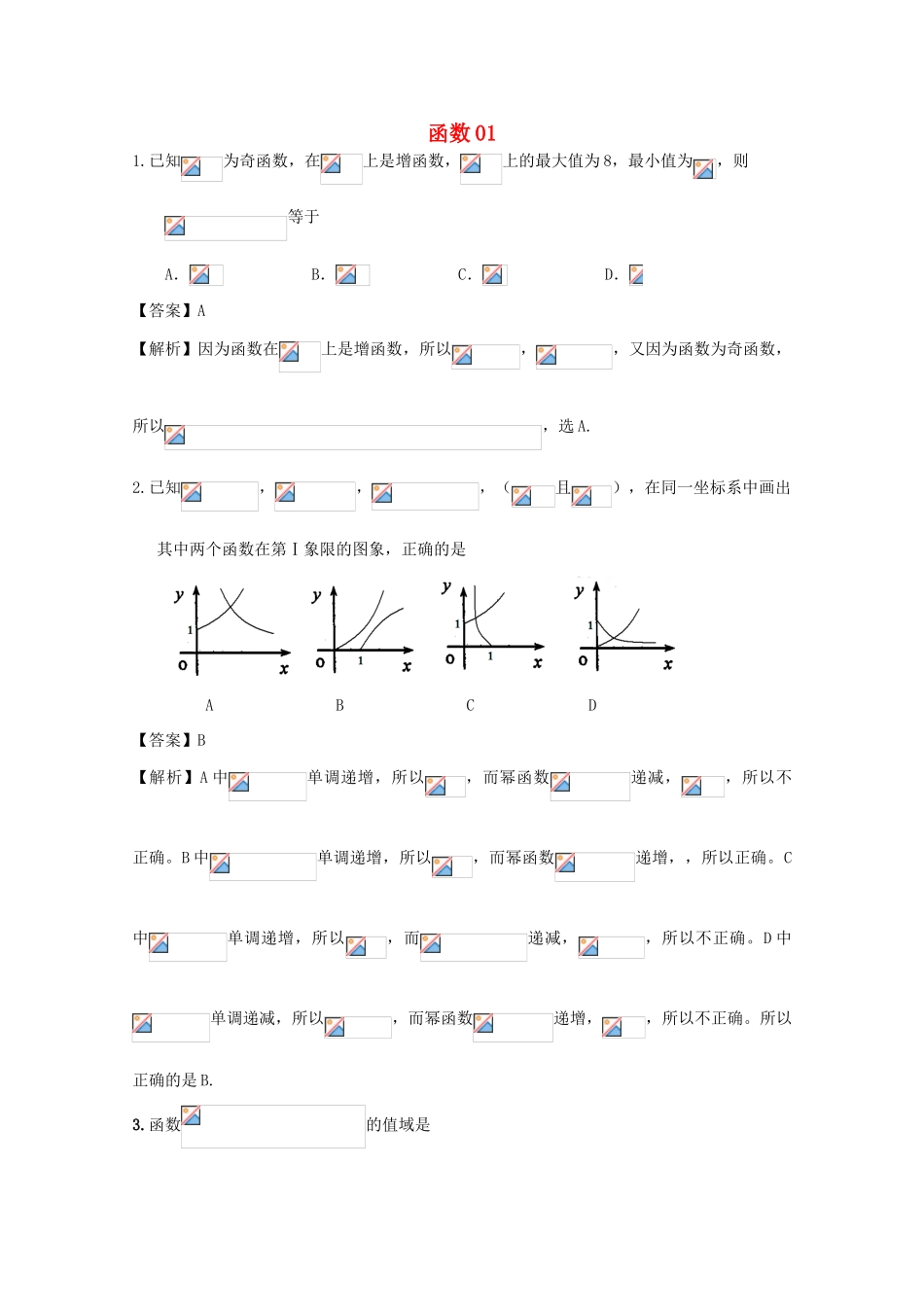
函数011.已知为奇函数,在上是增函数,上的最大值为8,最小值为,则等于A.B.C.D.【答案】A【解析】因为函数在上是增函数,所以,,又因为函数为奇函数,所以,选A.2.已知,,,(且),在同一坐标系中画出其中两个函数在第Ⅰ象限的图象,正确的是ABCD【答案】B【解析】A中单调递增,所以,而幂函数递减,,所以不正确。B中单调递增,所以,而幂函数递增,,所以正确。C中单调递增,所以,而递减,,所以不正确。D中单调递减,所以,而幂函数递增,,所以不正确。所以正确的是B.3.函数的值域是A.RB.(1,2)C.[2,+∞)D.(-,l)(2,+)【答案】A【解析】由,得或。所以函数的值域为R,选A.4.已知定义在上的奇函数,满足,且在区间上是增函数,若方程,在区间上有四个不同的根,则=A.-12B.-8C.-4D.4【答案】B【解析】因为是定义在R上的奇函数,满足,所以,由为奇函数,所以函数图象关于直线对称且,由知,所以函数是以8为周期的周期函数,又因为在区间[0,2]上是增函数,所以在区间[2−,0]上也是增函数.如图2所示,那么方程m(m>0)在区间[8−,8]上有四个不同的根x1,x2,x3,x4,不妨设x10,a≠1)的图象过区域M的的取值范围是A.[1,3]B.[,9]C.[2,9]D.[2,5]【答案】D【解析】由图象可知不等式组对应的平面区域为三角形,若,显然指数函数不过区域M.,所以必有,当指数函数经过点C时,最小,当指数函数经过点D时,最大。当时,,即点。当时,,即点。把,代入可得,把代入得,所以的取值范围是,即,选D.7.定义域为的偶函数满足对,有,且当时,,若函数在上至少有三个零点,则的取值范围是()A.B.C.D.【答案】B【解析】因为函数是偶函数,所以,即,所以函数关于直线对称,又,所以,即函数的周期是4.由得,,令,当时,,过定点.由图象可知当时,不成立.所以.因为,所以要使函数在上至少有三个零点,则有,即,所以,即,所以,即的取值范围是,选B,如图.8.已知定义域为R的函数满足,当时,单调递增,如果且,则的值()A.恒小于0B.恒大于0C.可能为0D.可正可负【答案】A【解析】因为函数满足,所以函数关于点对称,由,知异号。不妨设,则由得,而,当时,函数单调递增,根据函数的单调性可知,,即,所以,选A.9.函数的定义域是,则其值域是()A、B、C、D、【答案】A【解析】当时,,此时。当时,,此时,,即,综上函数的值域为,选A.10.设函数,若,则实数的取值范围是()A、B、C、D、【答案】C【解析】若,则由得,即,所以。若,则由得,,所以。综上的取值范围是,即,选C.11.已知函数,如果且,则它的图象可能是()【答案】D【解析】由且,得,所以抛物线开口向上,排除A,C.又,所以排除B,选D.12.若,例如则的奇偶性为()A.偶函数不是奇函数;B.奇函数不是偶函数;C.既是奇函数又是偶函数;D.非奇非偶函数;【答案】A【解析】由题意知,所以函数为偶函数,不是奇函数,选A.13.已知函数,则函数的零点所在的区间是A.(0,1)B.(1,2)C.(2,3)D.(3,4)【答案】B【解析】函数的导数为,所以。因为,,所以函数的零点所在的区间为.选B.14.已知函数:①,②,③.则以下四个命题对已知的三个函数都能成立的是命题是奇函数;命题在上是增函数;命题;命题的图像关于直线对称A.命题B.命题C.命题D.命题【答案】C【解析】当时,函数不是奇函数,所以命题不能使三个函数都成立,排除A,D.①成立;②成立;③成立,所以命题能使三个函数都成立,所以选C.