高中数学 第一章 三角函数 1.4.2 正弦函数、余弦函数的性质 三角函数的最值典例剖析 新人教A版必修4-新人教A版高一必修4数学试题VIP免费

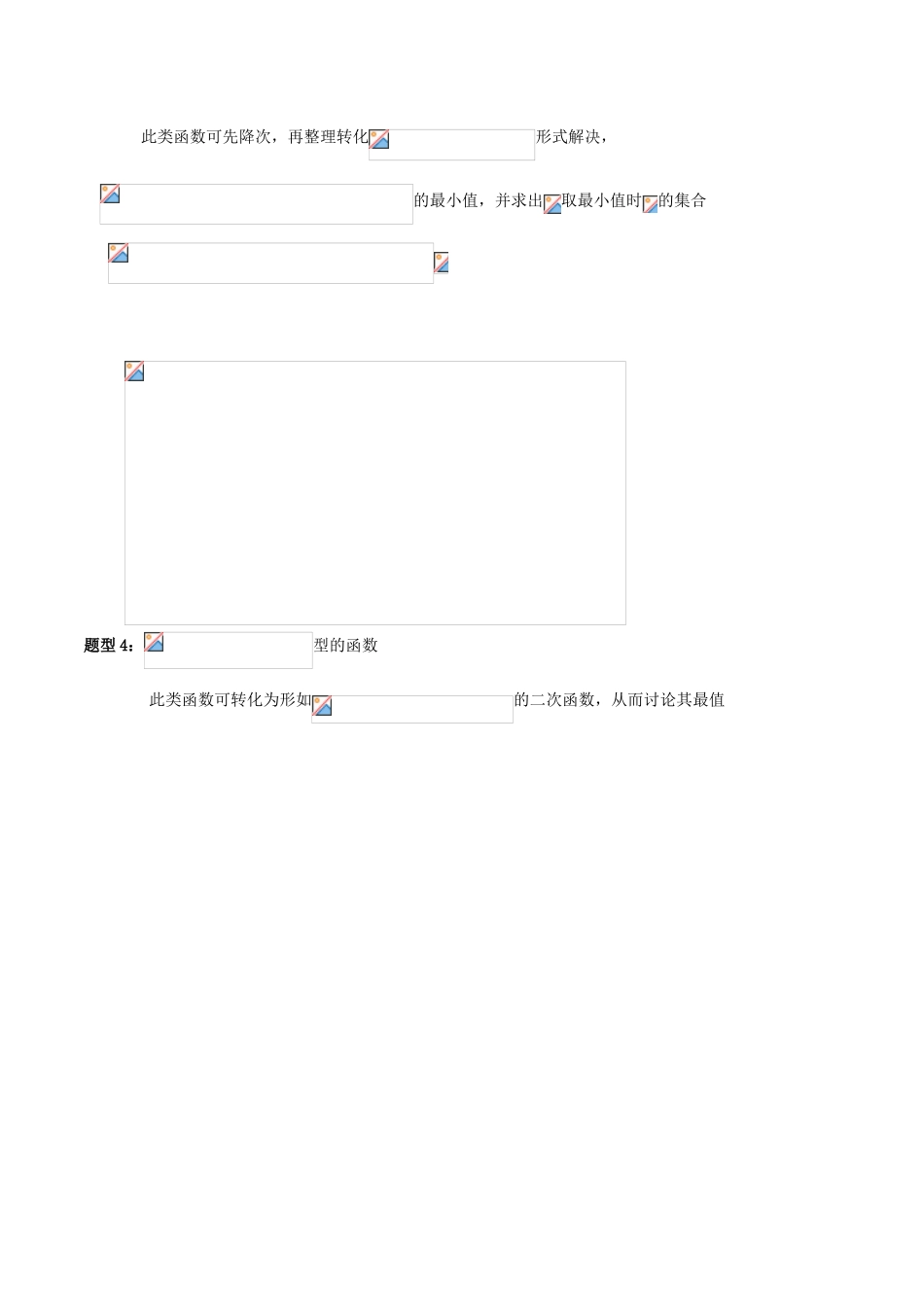
三角函数的最值典例剖析题型1：此类函数利用即可求解，显然[例1]求的最大值与最小值题型2：y=asinx+bcosx型可化为y=（其中）[例2]（2004年全国，理4）函数在区间[0，]上的最小值为____。[解析]：=2（）=2（）=2因为，所以，当时，易知y的最小值为[答案]所以应填“1”。题型3：型的函数此类函数可先降次，再整理转化形式解决，的最小值，并求出取最小值时的集合题型4：型的函数此类函数可转化为形如的二次函数，从而讨论其最值224:1cos24,0cos1,211,2,2yaaaxoxxaaa222max5a3例：是否存在常数a，使得函数y=sinx+acosx+-在闭区间上的最大值是1？82若存在求出对应的值？若不存在，试说明理由。5a35a3解析sinx+acosx+-cosxcosx+-82825a1-82时若即则当cosx=1时y2532012821321,3140423021210532aaaaaaaamaxmax舍去aa若0即0a2,则当cosx=时225a1y-或舍82即a<0,则当cosx=0时5a1y-舍82综合上述知，存在符合题设题型5：型的函数此类函数可转化为去处理，或利用万能公式换元后用判别式处理可看作是单位圆上的动点P与Q连线的斜率，设直线的方程为即，则圆心（0,0）到它的距离解得或【附】：求的值域（反解法）又函数的值域题型6：含有“的三角函数的最值问题。此类函数的常用解决方法是令将转化为的函数关系，最终划归为二次函数的最值问题。求函数的最值。题型7：利用函数单调性求最值求的最值及对应的的集合：将分子展开转化为的形式来解决令则且设