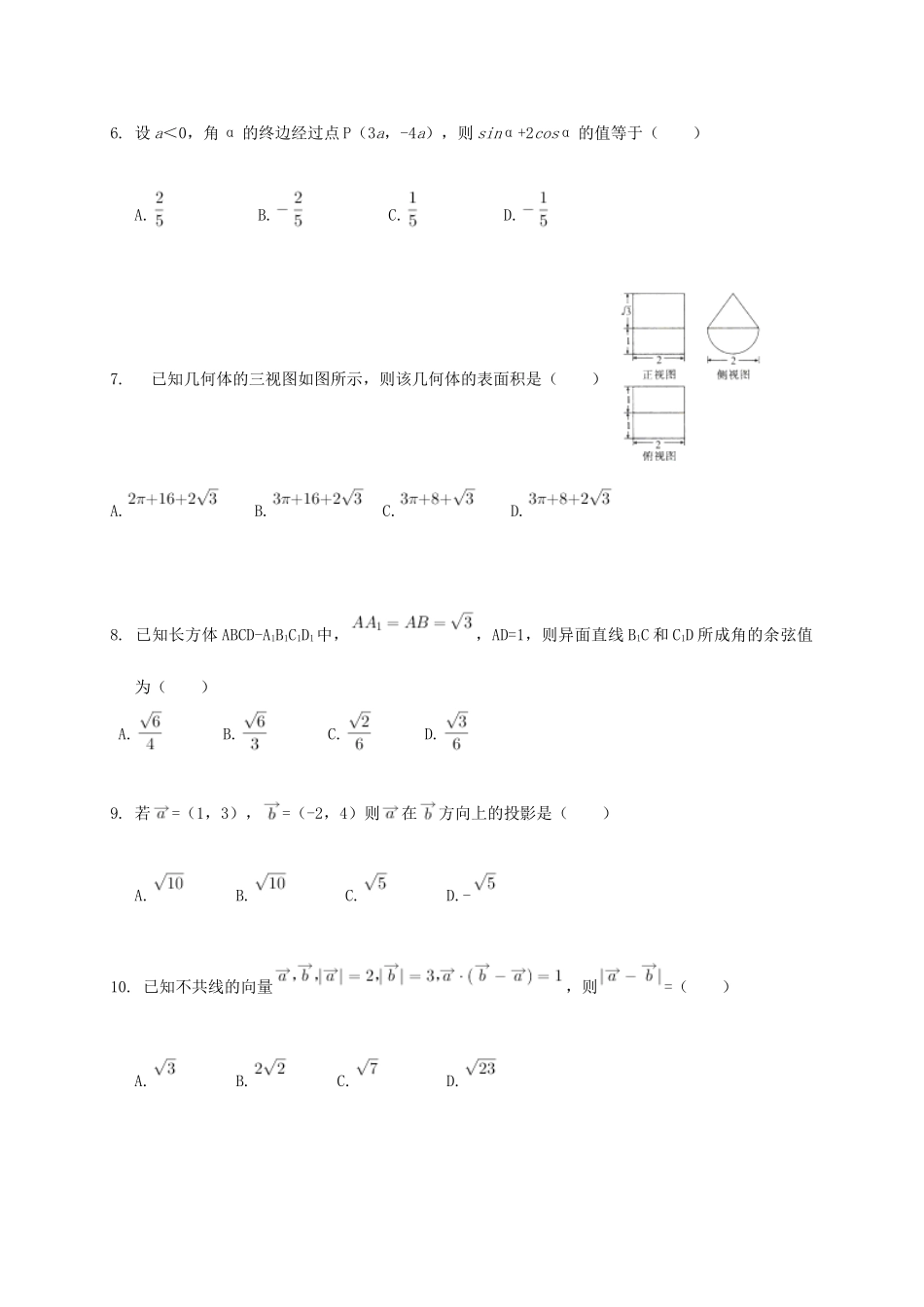
2016-2017学年度第二学期高一年级第二次月考数学试卷(理科)一.选择题(本大题共12小题,共60.0分)1.下列命题中正确的是()A.终边在x轴负半轴上的角是零角B.三角形的内角必是第一、二象限内的角C.不相等的角的终边一定不相同D.若β=α+k•360°(k∈Z),则α与β终边相同2.已知=(3,1),向量=(-4,-3),则向量=()A.(-7,-4)B.(7,4)C.(-1,4)D.(1,4)3.已知f(x)=,则f(-1)+f(4)的值为()A.-7B.-8C.3D.44.函数的定义域为()A.B.C.D.5.一艘轮船按照北偏西50°的方向,以15浬每小时的速度航行,一个灯塔M原来在轮船的北偏东10°方向上.经过40分钟,轮船与灯塔的距离是浬,则灯塔和轮船原来的距离为()A.2浬B.3浬C.4浬D.5浬6.设a<0,角α的终边经过点P(3a,-4a),则sinα+2cosα的值等于()A.B.C.D.7.已知几何体的三视图如图所示,则该几何体的表面积是()A.B.C.D.8.已知长方体ABCD-A1B1C1D1中,,AD=1,则异面直线B1C和C1D所成角的余弦值为()A.B.C.D.9.若=(1,3),=(-2,4)则在方向上的投影是()A.B.C.D.-10.已知不共线的向量,则=()A.B.C.D.11.已知是单位向量,||=,且(2+)•(-)=4-,则与的夹角为()A.45°B.60°C.120°D.135°12.已知向量=(cos5°,sin5°),,则=()A.1B.C.D.二、填空题(本大题共4小题,共20.0分)13.已知函数(x∈R).则函数函数y=f(x)的值域为______.14.设向量,若向量与平行,则m=______.15.已知△ABC的三内角A,B,C所对的边分别为a,b,c,且sinA=2sinC,b2=ac,则cosB=______.16.已知a、b、c分别为△ABC三个内角A、B、C的对边,若cosB=,a=5,△ABC的面积为12,则的值等于______三、解答题(本大题共6小题,共70.0分)17.在锐角△ABC的内角A,B,C的对边分别为a,b,c,且a=2csinA.(1)确定角C的大小;(2)若c=,且ab=6,求边a,b.18.已知△ABC的内角A,B,C的对边分别为a,b,c,若cosA=,c=3b,且△ABC面积S△ABC=.(1)求边b.c;(2)求边a并判断△ABC的形状.19.如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC;(2)求证:CO⊥面VAB;(3)求三棱锥C-VAB的体积.20.已知f(α)=.(1)若α是第三象限角,且cos(α-π)=,求f(α)的值;(2)若f(α)=-2,求2sinαcosα+cos2α的值.21.已知函数部分图象如图所示.(Ⅰ)求f(x)的最小正周期及图中x0的值;(Ⅱ)求f(x)在区间[0,]上的最大值和最小值.22.设函数f(x)=•,其中向量=(2cosx,1),=(cosx,sin2x),x∈R.(1)求f(x)的单调递增区间;(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知f(A)=2,b=1,△ABC的面积为,求c的值.高一数学第二次月考答案(理科)【答案】1.D2.A3.C4.D5.D6.B7.D8.A9.C10.A11.D12.D13.[-2,2]14.-15.16.17.(本小题满分10分)解:(1)由a=2csinA及正弦定理得==,-------(4分)(知道用正弦定理2分)因为sinA>0,故sinC=,又锐角△ABC,所以C=.---------------------------------------------(6分)(2)由余弦定理a2+b2-2abcos=7,-----------------(9分)(余弦定理2分)ab=6,得a2+b2=1,解得:或.-----------------------------------(12分)18.(本小题满分12分)解:(1) cosA=,∴sinA=.--------------(2分)又S△ABC=bcsinA=,∴bc=3.----------------(4分)又c=3b,∴b=1,c=3.-----------------------------------------(6分)(2)由余弦定理a2=b2+c2-2bccosA,-----(8分)得:a2=1+9-2×=8,故a=2.-----(10分)由c2=a2+b2知△ABC为直角三角形.-----------(12分)19.证明:(1) O,M分别为AB,VA的中点,∴VB∥OM,又VB⊄平面MOC,OM⊂平面MOC,∴VB∥平面MOC.(2) AC=BC,O是AB的中点,∴OC⊥AB,又平面VAB⊥平面ABC,平面VAB∩平面ABC=AB,OC⊂平面ABC,∴OC⊥平面VAB.(3) AC⊥BC且AC=BC=,∴AB=2.∴OC=AB=1. △VAB为等边三角形,∴S△VAB==.∴VC-VAB===.20.解:由f(α)== cos(α-π)=-sinα=,即sinα=α是第三象限角,∴cosα==那么f(α...