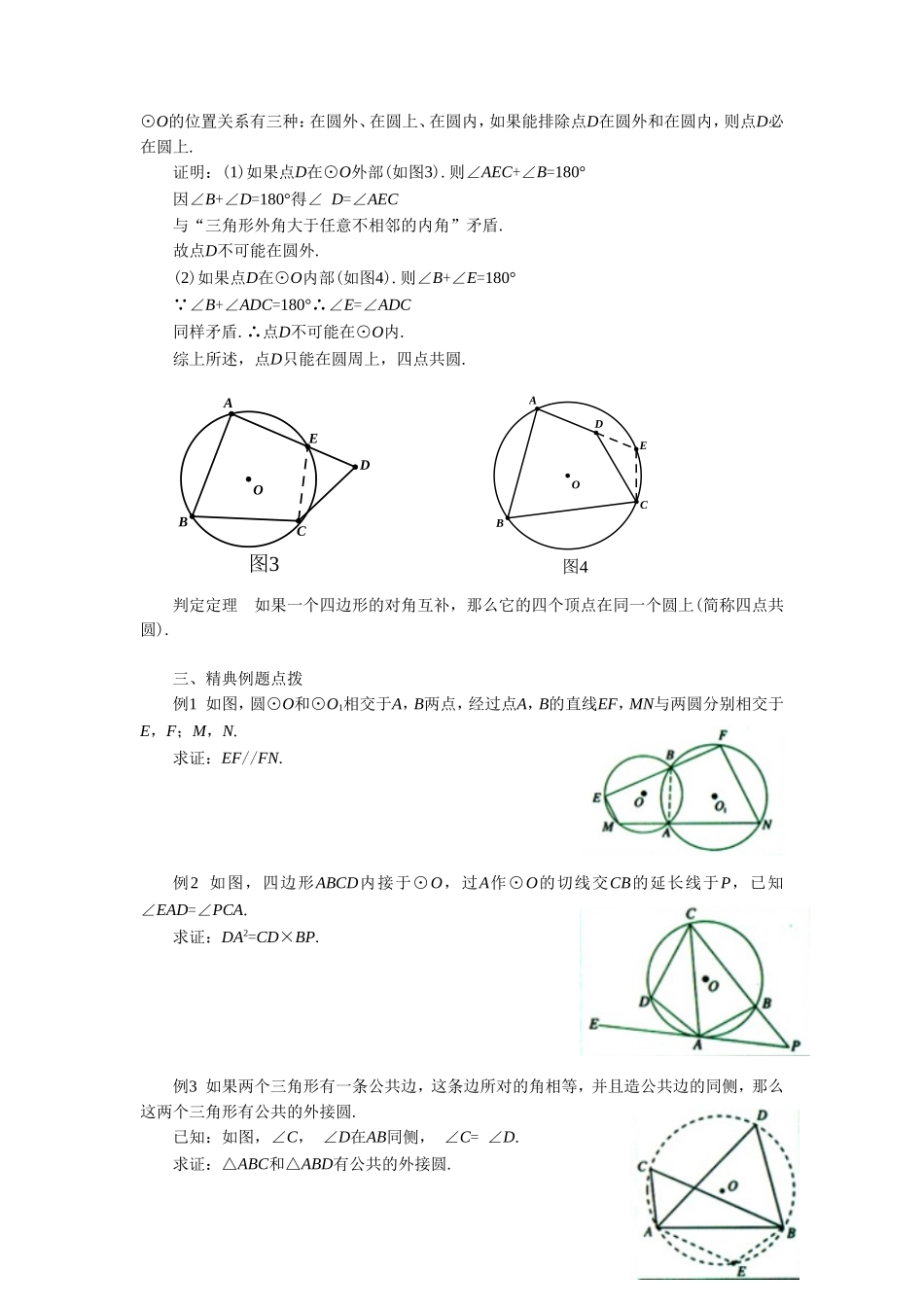
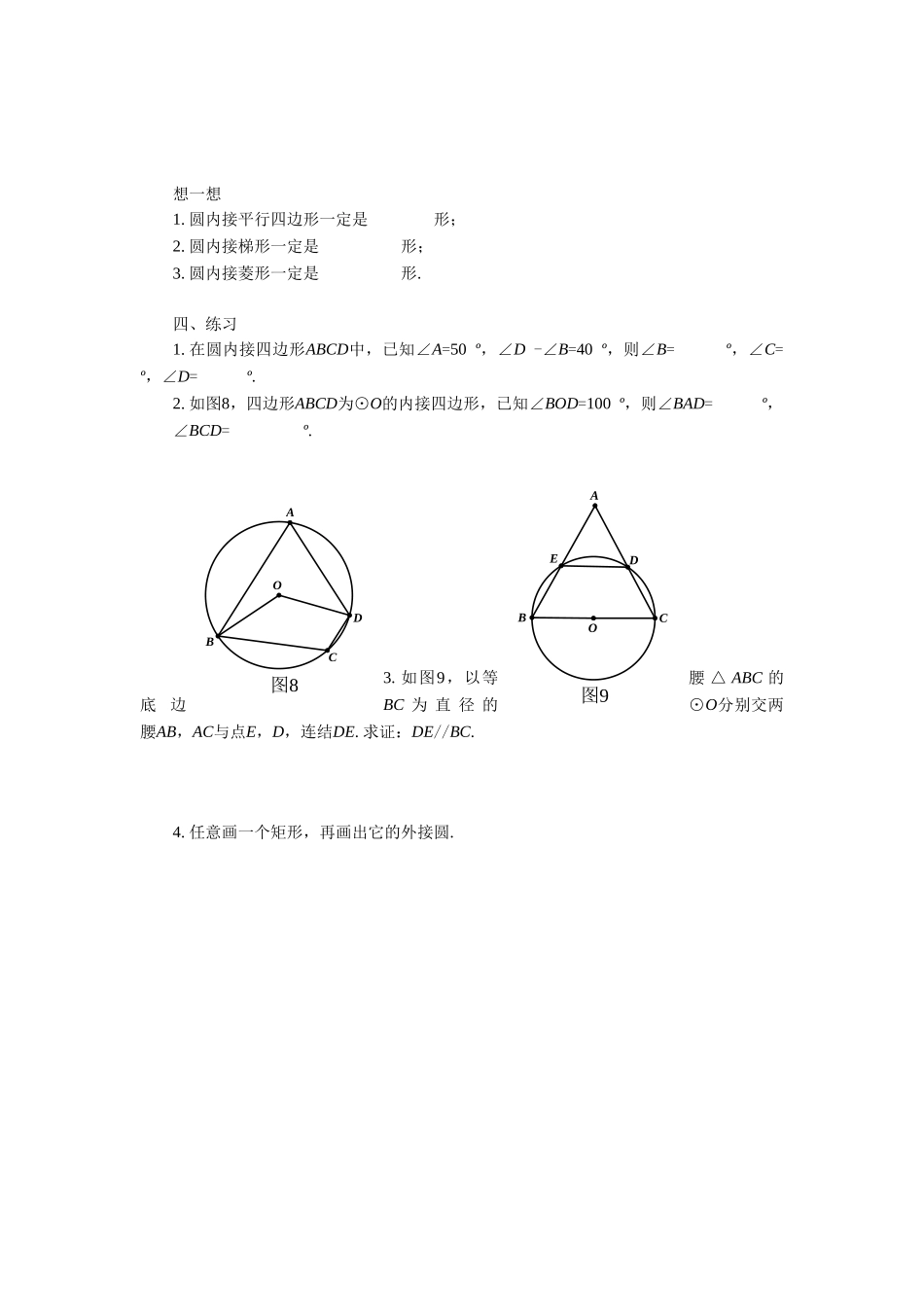
《1.3.2圆的内接四边形的性质与判定》导学案学习目标1.了解圆内接多边形和多边形外接圆的概念;掌握圆内接四边形的概念及其性质定理;2.掌握圆内接四边形判定定理及其推论;熟练运用圆内接四边形的性质与判定定理进行计算和证明.学习重难点圆内接四边形的性质与判定定理.自主学习一、基础知识回顾1.在同圆或等圆中,相等的圆心角所对的相等,所对的也相等.2.在同圆或等圆中,如果两个圆心角、两条、两条、两个中有一对量相等,那么它们所对应的其余各对量都相等.3.圆周角定理:一条弧所对的圆周角等于它所对.(1)半圆(或直径)所对的圆周角是;90º的圆周角所对的弦是.(2)在同圆或等圆中,同弧或等弧所对的圆周角;相等的圆周角所对的弧也.二、知识延伸拓展如果四边形的各顶点在一个圆上,这个四边形叫做这个圆的内接四边形,这个圆叫做四边形的外接圆.例如,图1中,四边形ABCD是⊙O的内接四边形;⊙O是四边形ABCD的外接圆.圆内接四边形有以下性质:性质定理圆的内接四边形的对角互补,并且任何一个外角都等于它的相邻内角的对角.已知:如图2,四边形ABCD内接于⊙O,∠DCE是四边形ABCD的外角.求证:(1)∠A+∠BCD=180º,∠B+∠D=180º;(2)∠DCE=∠A.证明:(1)反过来,如果一个四边形的对角互补,那么它的四个顶点在同一个圆上吗?已知:四边形ABCD中,∠B+∠D=180°求证:A,B,C,D在同一圆周上.分析:根据不在同一直线上的三点确定一个圆,不妨设A、B、C三点确定⊙O,则点D与OABCD图1OABCDE图2⊙O的位置关系有三种:在圆外、在圆上、在圆内,如果能排除点D在圆外和在圆内,则点D必在圆上.证明:(1)如果点D在⊙O外部(如图3).则∠AEC+∠B=180°因∠B+∠D=180°得∠D=∠AEC与“三角形外角大于任意不相邻的内角”矛盾.故点D不可能在圆外.(2)如果点D在⊙O内部(如图4).则∠B+∠E=180°∵∠B+∠ADC=180°∴∠E=∠ADC同样矛盾.∴点D不可能在⊙O内.综上所述,点D只能在圆周上,四点共圆.判定定理如果一个四边形的对角互补,那么它的四个顶点在同一个圆上(简称四点共圆).三、精典例题点拨例1如图,圆⊙O和⊙O1相交于A,B两点,经过点A,B的直线EF,MN与两圆分别相交于E,F;M,N.求证:EF//FN.例2如图,四边形ABCD内接于⊙O,过A作⊙O的切线交CB的延长线于P,已知∠EAD=∠PCA.求证:DA2=CD×BP.例3如果两个三角形有一条公共边,这条边所对的角相等,并且造公共边的同侧,那么这两个三角形有公共的外接圆.已知:如图,∠C,∠D在AB同侧,∠C=∠D.求证:△ABC和△ABD有公共的外接圆.图3EOCDAB图4EODABC想一想1.圆内接平行四边形一定是形;2.圆内接梯形一定是形;3.圆内接菱形一定是形.四、练习1.在圆内接四边形ABCD中,已知∠A=50º,∠D-∠B=40º,则∠B=º,∠C=º,∠D=º.2.如图8,四边形ABCD为⊙O的内接四边形,已知∠BOD=100º,则∠BAD=º,∠BCD=º.3.如图9,以等腰△ABC的底边BC为直径的⊙O分别交两腰AB,AC与点E,D,连结DE.求证:DE//BC.4.任意画一个矩形,再画出它的外接圆.图8OABDC图9DEOABC