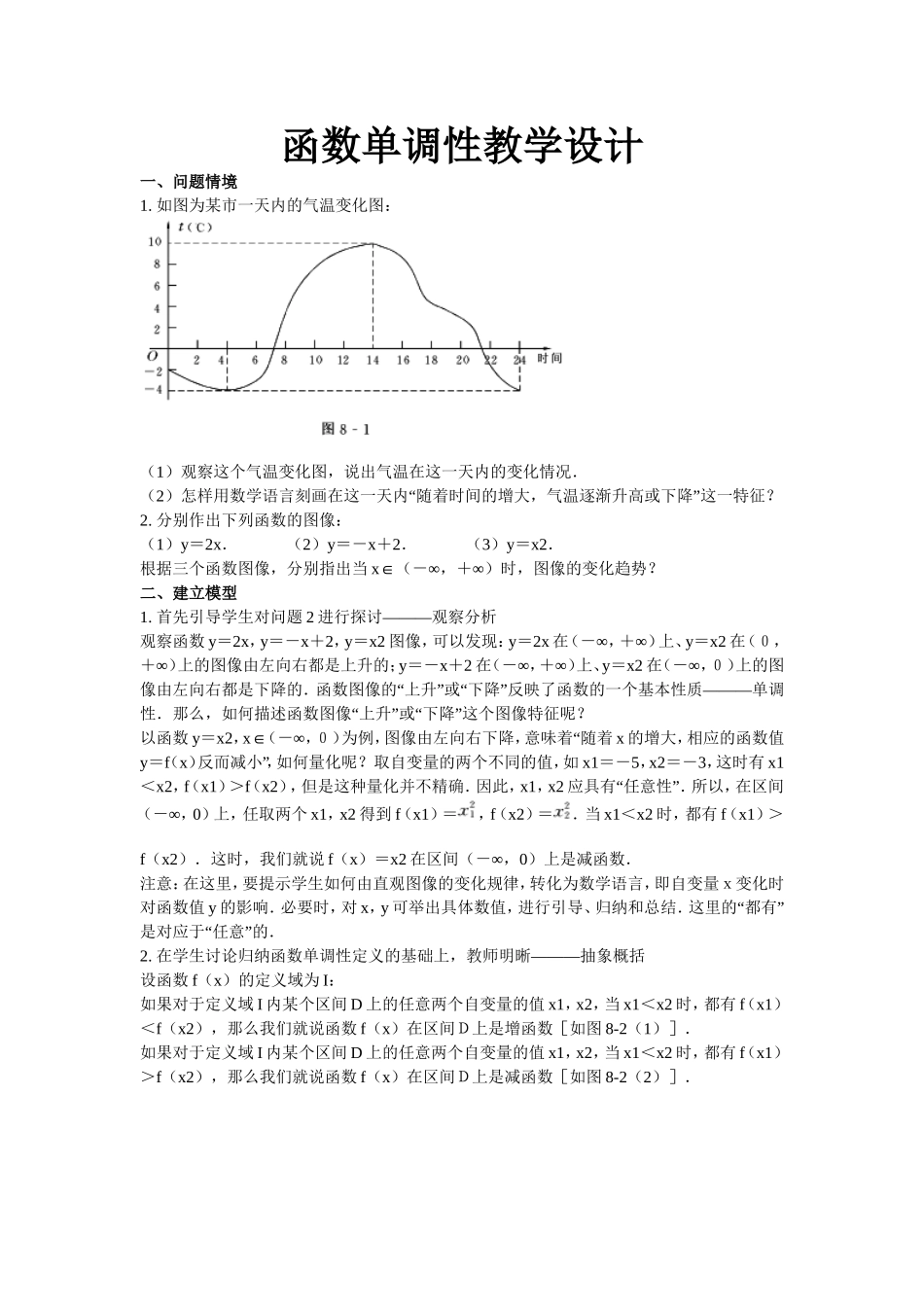
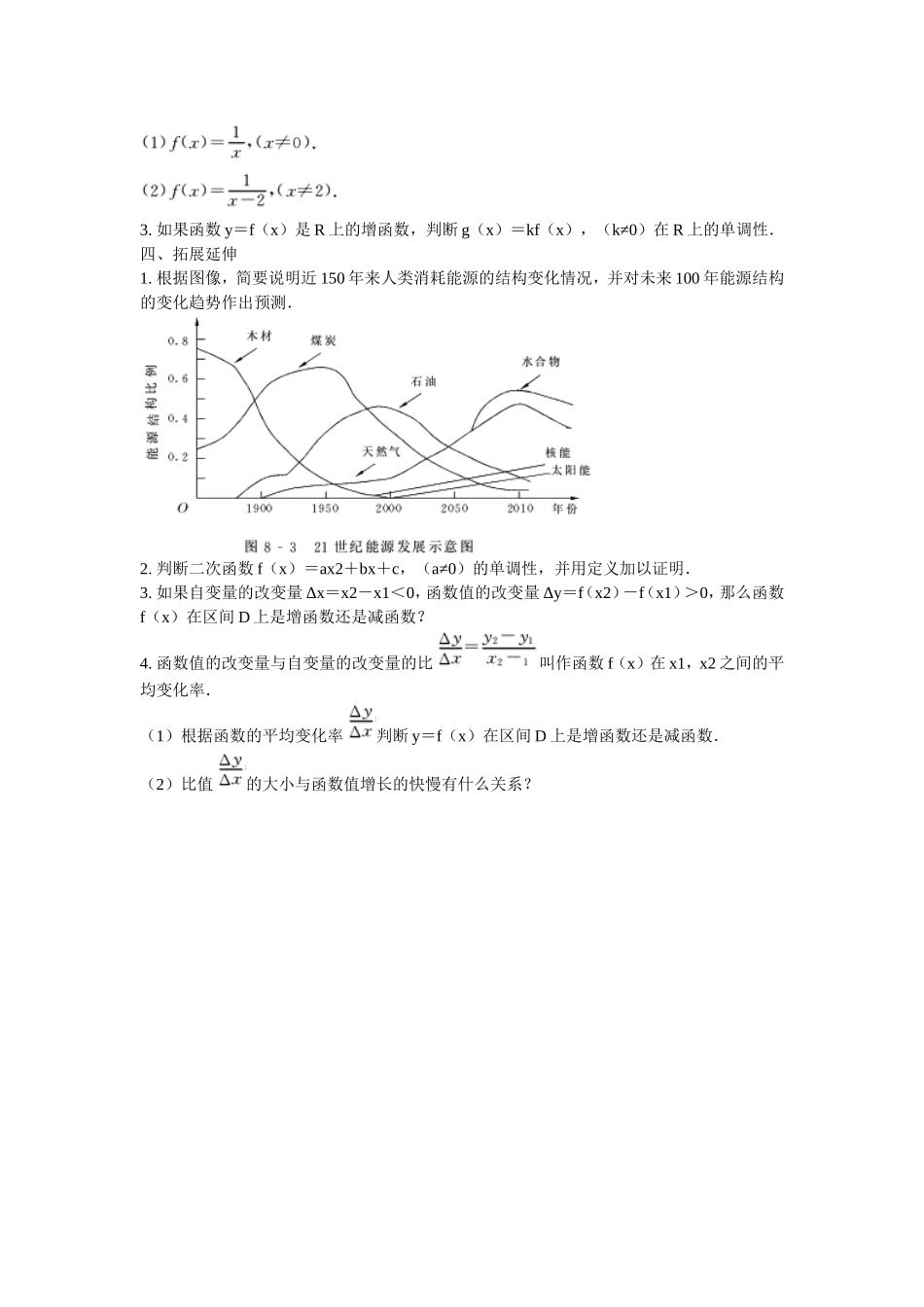
函数单调性教学设计一、问题情境1.如图为某市一天内的气温变化图:(1)观察这个气温变化图,说出气温在这一天内的变化情况.(2)怎样用数学语言刻画在这一天内“随着时间的增大,气温逐渐升高或下降”这一特征?2.分别作出下列函数的图像:(1)y=2x.(2)y=-x+2.(3)y=x2.根据三个函数图像,分别指出当x∈(-∞,+∞)时,图像的变化趋势?二、建立模型1.首先引导学生对问题2进行探讨———观察分析观察函数y=2x,y=-x+2,y=x2图像,可以发现:y=2x在(-∞,+∞)上、y=x2在(0,+∞)上的图像由左向右都是上升的;y=-x+2在(-∞,+∞)上、y=x2在(-∞,0)上的图像由左向右都是下降的.函数图像的“上升”或“下降”反映了函数的一个基本性质———单调性.那么,如何描述函数图像“上升”或“下降”这个图像特征呢?以函数y=x2,x∈(-∞,0)为例,图像由左向右下降,意味着“随着x的增大,相应的函数值y=f(x)反而减小”,如何量化呢?取自变量的两个不同的值,如x1=-5,x2=-3,这时有x1<x2,f(x1)>f(x2),但是这种量化并不精确.因此,x1,x2应具有“任意性”.所以,在区间(-∞,0)上,任取两个x1,x2得到f(x1)=,f(x2)=.当x1<x2时,都有f(x1)>f(x2).这时,我们就说f(x)=x2在区间(-∞,0)上是减函数.注意:在这里,要提示学生如何由直观图像的变化规律,转化为数学语言,即自变量x变化时对函数值y的影响.必要时,对x,y可举出具体数值,进行引导、归纳和总结.这里的“都有”是对应于“任意”的.2.在学生讨论归纳函数单调性定义的基础上,教师明晰———抽象概括设函数f(x)的定义域为I:如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么我们就说函数f(x)在区间D上是增函数[如图8-2(1)].如果对于定义域I内某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么我们就说函数f(x)在区间D上是减函数[如图8-2(2)].如果函数y=f(x)在区间D上是增函数或减函数,那么我们就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫作y=f(x)的单调区间.3.提出问题,组织学生讨论(1)定义在R上的函数f(x),满足f(2)>f(1),能否判断函数f(x)在R是增函数?(2)定义在R上函数f(x)在区间(-∞,0]上是增函数,在区间(0,+∞)上也是增函数,判断函数f(s)在R上是否为增函数.(3)观察问题情境1中气温变化图像,根据图像说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数.强调:定义中x1,x2是区间D上的任意两个自变量;函数的单调性是相对于某一区间而言的.三、解释应用[例题]1.证明函数f(x)=2x+1,在(-∞,+∞)是增函数.注:要规范解题格式.2.证明函数f(x)=,在区间(-∞,0)和(0,+∞)上都是减函数.思考:能否说,函数f(x)=在定义域(-∞,0)∪(0,+∞)上是减函数?3.设函数y=f(x)在区间D上保号(恒正或恒负),且f(x)在区间D上为增函数,求证:f(x)=在区间D上为减函数.证明:设x1,x2∈D,且x1<x2,∵f(x)在区间D上保号,∴f(x1)f(x2)>0.又f(x)在区间D上为增函数,∴f(x1)-f(x2)<0,从而g(x1)-g(x2)>0,∴g(x)在D上为减函数.[练习]1.证明:(1)函数f(x)=在(0,+∞)上是增函数.(2)函数f(x)=x2-x在(-∞,]上是减函数.2.判断函数的单调性,并写出相应的单调区间.3.如果函数y=f(x)是R上的增函数,判断g(x)=kf(x),(k≠0)在R上的单调性.四、拓展延伸1.根据图像,简要说明近150年来人类消耗能源的结构变化情况,并对未来100年能源结构的变化趋势作出预测.2.判断二次函数f(x)=ax2+bx+c,(a≠0)的单调性,并用定义加以证明.3.如果自变量的改变量Δx=x2-x1<0,函数值的改变量Δy=f(x2)-f(x1)>0,那么函数f(x)在区间D上是增函数还是减函数?4.函数值的改变量与自变量的改变量的比叫作函数f(x)在x1,x2之间的平均变化率.(1)根据函数的平均变化率判断y=f(x)在区间D上是增函数还是减函数.(2)比值的大小与函数值增长的快慢有什么关系?