26.1.2反比例函数的图象和性质(1).1.2反比例函数的图象和性质(1)VIP免费

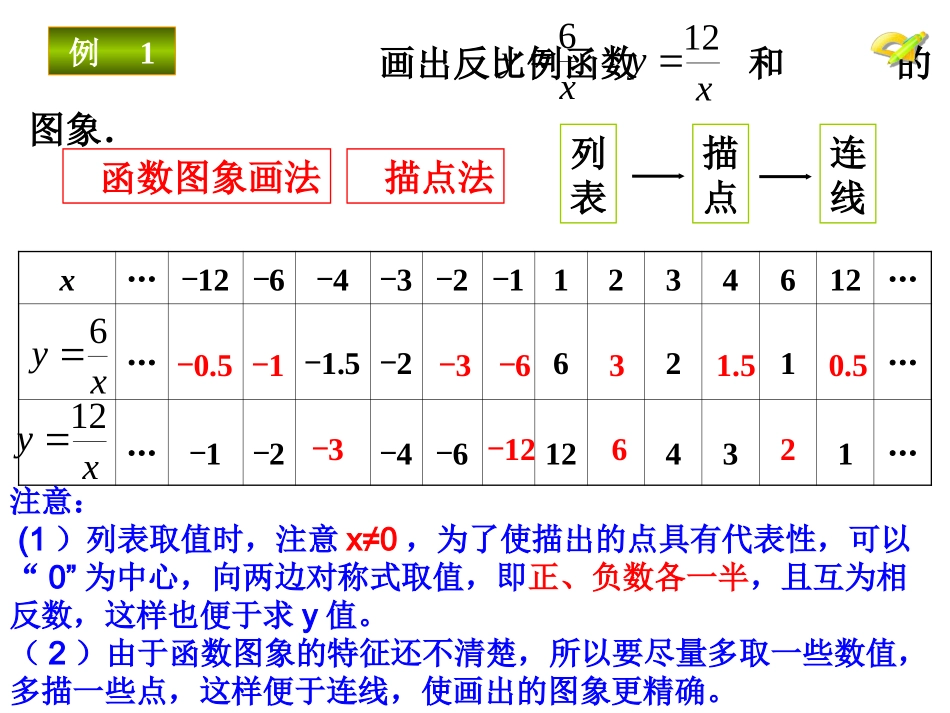
26.1.2反比例函数的图像和性质（1）课前检测课前检测1、过点（2，5）的反比例函数的解析式是：.2、一次函数y=2x-1的图象是，y随x的增大而.3、用描点法作函数图象的步骤：___________________________10yx一条直线增大列表，描点，连线画出反比例函数和的图象．函数图象画法列表描点连线描点法xy6xy12x…-12-6-4-3-2-11234612……-1.5-2621……-1-2-4-612431…xy6xy1231.5-6-3-1-0.5-126-320.5例1注意：(1）列表取值时，注意x≠0，为了使描出的点具有代表性，可以“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y值。（2）由于函数图象的特征还不清楚，所以要尽量多取一些数值，多描一些点，这样便于连线，使画出的图象更精确。246-2-6-4246-2-4-60yxxy=x6123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.561.2112-1-6-2-3-3-1.5-2-4-6-1.2-12-1…………12-12-66-44-33-22-1-1……y=x6xy12········xy12反比例函数的图像由两条曲线组成，它是双曲线246-2-6-4246-2-4-60yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xyy=x6········xy121、每个函数的图像分别位于那些象限？2、在每一个象限内，y随x的变化如何变化？你能由它们的解析式说明道理？3．对于反比例函数，考虑问题（1）（2),你能得出同样的结论吗？)0(kxky（1）函数的图象分别位于第一、三象限；（1）函数的图象分别位于第一、三象限；结论：结论：一般地，当k＞0时，对于反比例函数一般地，当k＞0时，对于反比例函数xky（2）在每一个象限内，y值随x值的增大而减小。（2）在每一个象限内，y值随x值的增大而减小。小组合作回顾前面讨论反比例函数的图像和性质的过程，你能用类似的方法研究反比例函数的图像和性质吗？)0(kxky)0(kxky★★123456-1-3-2-4-5-61234-1-2-3-40-6-556yxxy=x6123456-16-2-3-4-5-6……-63-32-21.5-1.51.2-1.21-1……y=-x6画出反比例函数的函数图象。画出反比例函数的函数图象。xy6（1）函数的图象分别位于第二、四象限；（1）函数的图象分别位于第二、四象限；结论：结论：一般地，当k＜0时，对于反比例函数一般地，当k＜0时，对于反比例函数xky（2）在每一个象限内，y值随x值的增大而增大。（2）在每一个象限内，y值随x值的增大而增大。K>0K<0当k＞0时，函数图象的两个分支分别在第一、三象限，在每个象限内，y随x的增大而减小.当k＜0时，函数图象的两个分支分别在第二、四象限，在每个象限内，y随x的增大而增大.1.反比例函数的图象是双曲线;2.图象性质见下表：图象性质y=xk反比例函数的图象和性质：（课本P6练习）1、（1）下列图像中是反比例函数的图像的是（）C（A）y=5x（B）y=2x+3（C）（D）4yx3yx（2）如图，这是下列四个函数中哪一个函数的图象（）C(2)已知反比例函数的图象如图所示，则k0，且在图象的每一支上，y随x的增大而．（1）反比例函数y=-的图象在第_____象限.x52、填空：xky＜增大二、四1.通过本节课的学习，你有什么收获？还有什么困惑吗？2.你对自己本节课的表现满意吗？为什么？数缺形时少直觉，形少数时难入微．1、反比例函数y=-的图象是_______，分布在第_______象限，在每个象限内，y都随x的增大而_____.x2双曲线二、四增大2、写一个反比例函数__________,使它的图象在第一、三象限内。2、写一个反比例函数__________,使它的图象在第一、三象限内。答案不唯一答案不唯一3、下列函数中，当x＞0时，y随x的增大而减小的是()．(A)y＝x(B)(C)(D)y＝2xBxy1xy14.反比例函数（K为常数）图象位于（）Ａ．第一、二象限Ｂ．第一、三象限Ｃ．第二、四象限Ｄ．第三、四象限xky12C5、已知反比例函数的图象在第二、四象限内，函数图象上有两点，，则与的大小关系为（）A．y1>y2B．y1=y2C．y1