1.3二次方程根与系数关系VIP免费

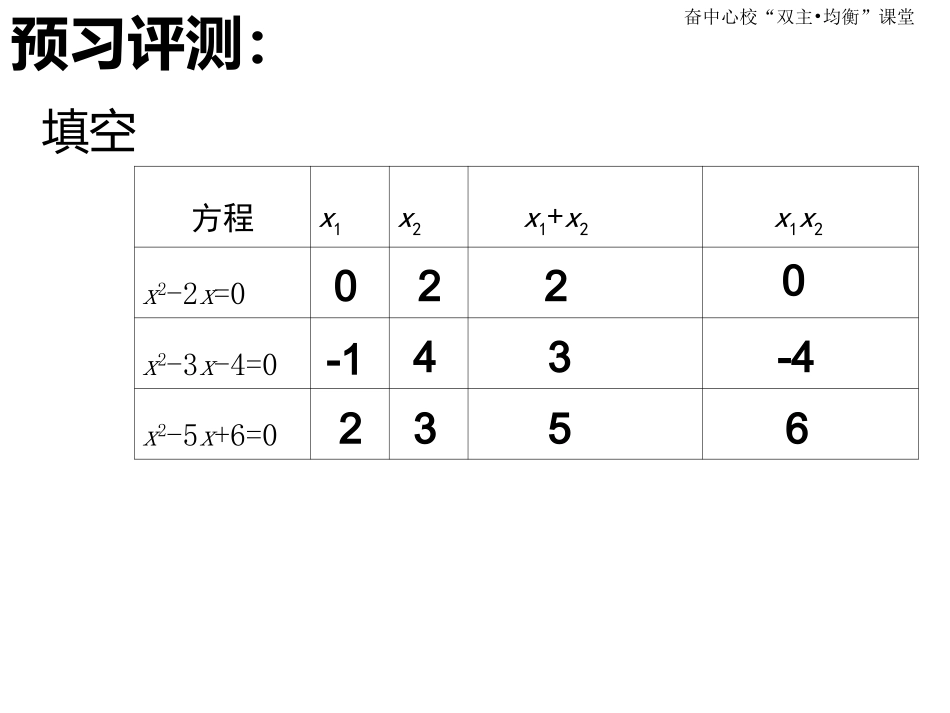
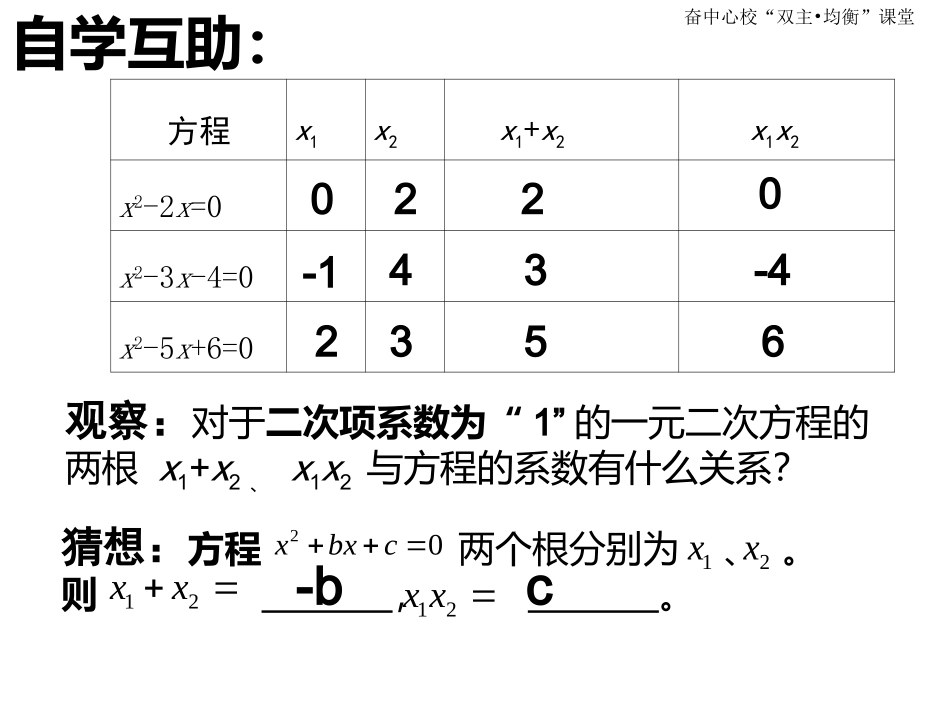
1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系周奋中心校“双主•均衡”课堂预习评测：方程x1x2x1+x2x1x2x2-2x=0x2-3x-4=0x2-5x+6=0填空0220-143-42356奋中心校“双主•均衡”课堂自学互助：方程x1x2x1+x2x1x2x2-2x=0x2-3x-4=0x2-5x+6=00220-143-42356观察：对于二次项系数为“1”的一元二次方程的两根x1+x2、x1x2与方程的系数有什么关系？猜想：方程两个根分别为、。则，。20xbxc1x2x12xx12xx-bc奋中心校“双主•均衡”课堂（2）填空方程x1x2x1+x2x1x22x2+x-3=05x2-9x-2=013212322159525观察:一元二次方程的2个根与系数的关系。猜想：当二次项系数不为“1”时,方程两个根分别为、。20(0)axbxca1x2x则，。12xx12xxbaca奋中心校“双主•均衡”课堂（3）若方程的两根分别为、。证明：（1）（2）20(0)axbxca1x2x12bxxa12cxxa奋中心校“双主•均衡”课堂展示点拨：1、列结论是否正确？若不正确请改正。2121215605（）设、是一元二次方程的两个根，则+=；xxxxxx212122311（）设、是一元二次方程的两个根，则=；xxxxxx2、求下列方程的两根的和与两根的积：2214102232（）；（）；xxxx3、如果-1是方程2x2－x+m=0的一个根，求另一个根。4、若方程的两个根为、。且，求m的取值范围。2210xxm1x2x120xx奋中心校“双主•均衡”课堂发展提高：设x1、x2是方程x2－4x+1=0的两个根，求下列各式的值。2212(1)xx212(2)()xx2211(3)2(51)xxx212122xxxx212124xxxx22111241xxxx212xx奋中心校“双主•均衡”课堂练习：完成导学案检测反馈奋中心校“双主•均衡”课堂归纳总结：归纳总结：通过本节课的学习你有通过本节课的学习你有哪些收获和疑问？哪些收获和疑问？