反比例函数图像VIP免费

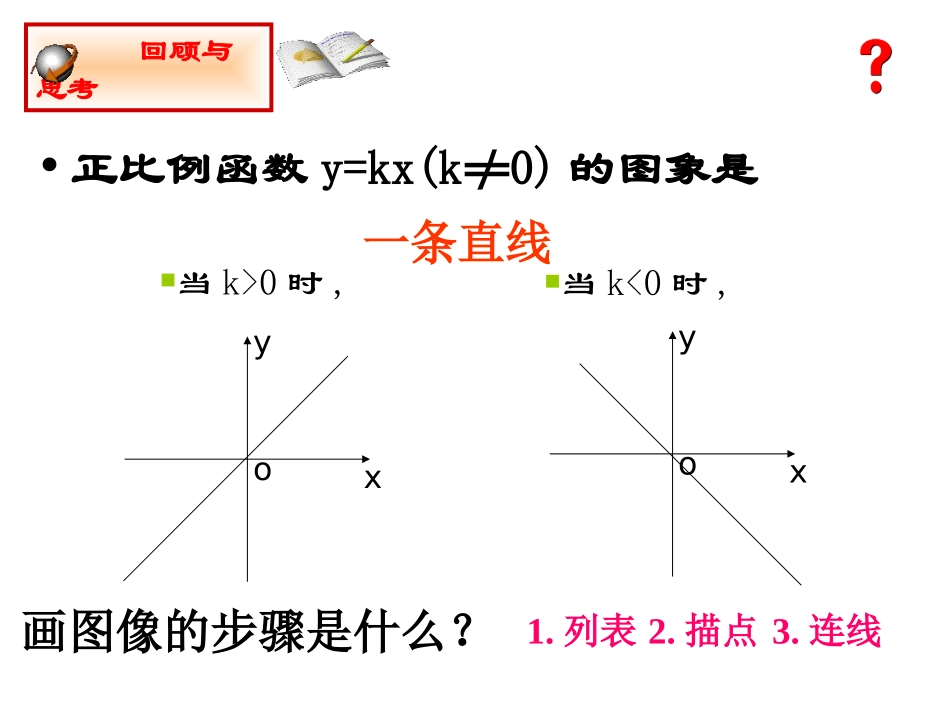
第五章第二课时反比例函数的图象与性质（1）复习提问1.下列函数中哪些是反比例函数？①②③④⑤⑥⑦⑧y=3x-1y=2x2y=x1y=2x3y=3xy=x1y=13xy=32x2.上节课我们学的反比例函数解析式是什么？(1)自变量x的取值范围是什么？(2)函数y的取值范围是什么？x≠0，y≠0kyx=（k≠0，k是常数）回顾与思考•正比例函数y=kx(k≠0)的图象是xyoxyo当k>0时,当k<0时,一条直线画图像的步骤是什么？1.列表2.描点3.连线反比例函数(k≠0)的图象是什么样子呢？xky让我们一起画个反比例函数的图象看看。作反比例函数的图象yx=41.列表x-8-4-3-2-112348yx=4-1-43-2-4-8424318例题122121213．连线：x-8-4-3-2-1-12348Y=--212121-134-2-4-884213421yx-1-2-3-4-5-6-7-887654321-8–7–6–5–4–3-2-1O12345678●●●●●●●●●●●●X42．描点：Y=4/X的函数曲线-12.5-10-7.5-5-2.502.557.51012.5-2.5-2-1.5-1-0.500.511.522.5议一议:你认为作反比例函数图象时应注意哪些问题?与同伴交流.注意：1.在列表时,自变量的值可以选取绝对值相等而符号相反的一对一对的数值,这样既可简化计算,又便于描点.2.列表、描点时,要尽量多取一些点,这样方便连线.3.连线时必须用光滑的曲线连接各点.4.描点时一定要养成按自变量从小到大的顺序依次画线,从中体会函数的增减性；5.曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交.作反例函数的图像y=x4-123456-4-1-2-3-5-6124563-6-5-1-3-4-20yx34-2121--1-2-4-88421213421-x…-8-4-3-2-1…12348…………．．．....．．．..y=x4-y=x4-想一想根据刚才的结论，对比下面两个反比例函数图像，他们有什么相同点和不同点？x反比例函数y=—的图象是由两支曲线组成的。xk(1)当k>0时，两支曲线分别位于第___、___象限，(2)当k<0时，两支曲线分别位于第___、___象限.一三二四y=4xy01yx01y=-4x双曲线反之？1.下列函数中，其图象位于第一、三象限的有___________；其图象在二、四象限内的是_______.x21x3.0x10x1007-（1）y＝；（2）y＝（3）y＝；（4）y＝.思考分析（1）（2）（3）（4）A：xyoB：xyoD：xyoC：xyo1、反比例函数y=-的图象大致是（）x5D1.函数的图像在第_____象限，函数的图象在第象限。2.双曲线经过点（-3，___）y=x5y=13x3.函数的图像在二、四象限，则m的取值范围是____.4.函数,它的图像在一、三象限，则m=____.（此函数是反比例函数）m-2xy=y=(2m+1)xm+2m-162试本领二,四m<2391yx=5一、三