二次函数-的图象和性质.3.2-二次函数y=a(x+h)2-的图像与性质VIP免费

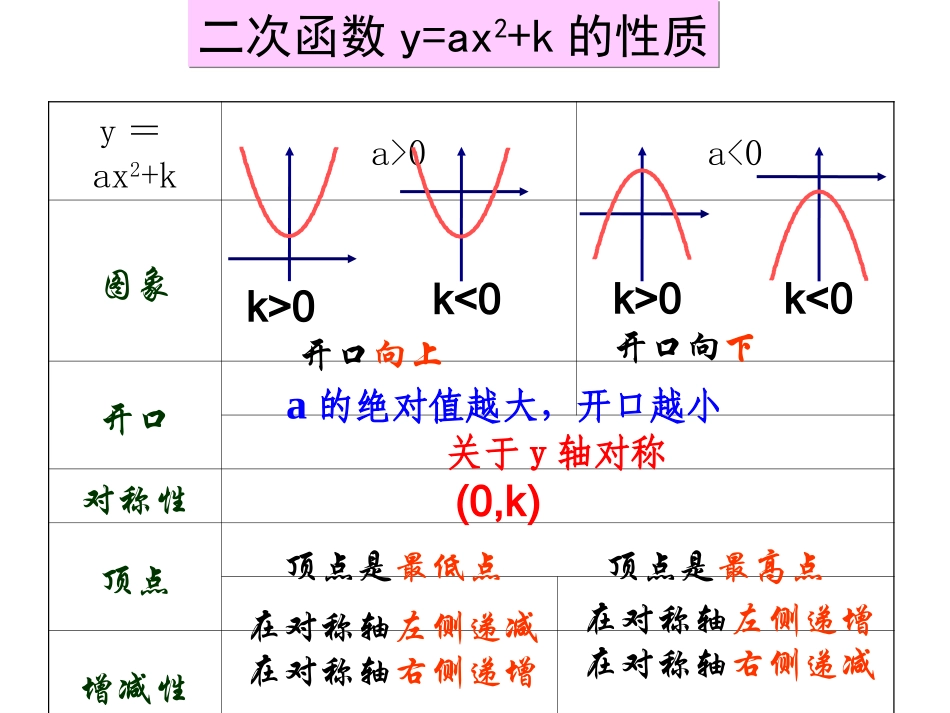
二次函数y=a(x+h)2的图象和性质y＝ax2+ka>0a<0图象开口对称性顶点增减性二次函数y=ax2+k的性质二次函数y=ax2+k的性质开口向上开口向下a的绝对值越大，开口越小关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减在对称轴右侧递增在对称轴左侧递增在对称轴右侧递减k>0k<0k<0k>0(0,k)x…-3-2-10123…解:先列表描点画出二次函数、的图像,并考虑它们的开口方向、对称轴和顶点.:21(1)2yx21(1)2yx2)1(21xy2)1(21xy12345x-1-2-3-4-5-6-7-8-91yo-1-2-3-4-5-10-2…0-0.5-2-0.5-8…-4.5-8…-2-0.50-4.5-2…-0.521(1)2yxx=－1(1)抛物线与的开口方向、对称轴、顶点?21(1)2yx21(1)2yx(2)抛物线有什么关系？以及增减性是怎么变化的？2)1(21xy2)1(21xy221xy21(1)2yxx=1抛物线与抛物线有什么关系?2)1(21xy2)1(21xy12345x-1-2-3-4-5-6-7-8-91yo-1-2-3-4-5-1021(1)2yx21(1)2yx2)1(21xy向左平移1个单位2)1(21xy212yx221xy221xy221xy向右平移1个单位即:在对称轴左侧递增在对称轴右侧递减一般地,抛物线y=a(x+h)2有如下特点:(1)对称轴是x=-h;(2)顶点是(-h,0).（3）抛物线y=a(x+h)2可以由抛物线y=ax2向左或向右平移|h|得到.h>0，向左平移;h<0，向右平移xy左加右减顶点(0,0)顶点(2,0)直线x=－2直线x=2654321-1-2-3-4-8-6-4-2246B221xy2221xy2221xy221xy向右平移2个单位向左平移2个单位2)2(21xy2)2(21xy顶点(－2,0)对称轴:y轴即直线:x=0在同一坐标系中作出下列二次函数:221xy2)2(21xy2)2(21xy观察三条抛物线的相互关系,并分别指出它们的开口方向,对称轴及顶点.向右平移2个单位向右平移2个单位向左平移2个单位向左平移2个单位y＝a(x-ｈ)2a>0a<0图象开口对称性顶点增减性二次函数y=a（x+ｈ）2的性质二次函数y=a（x+ｈ）2的性质开口向上开口向下a的绝对值越大，开口越小直线ｘ＝-ｈ顶点是最低点顶点是最高点在对称轴左侧递减在对称轴右侧递增在对称轴左侧递增在对称轴右侧递减h>0h<0h<0h>0(-ｈ,0)填空题（1）二次函数y=2（x+5）2的图像是，开口对称轴是，当x=时，y有最值，是.（2）二次函数y=-3（x-4）2的图像是由抛物线y=-3x2向平移个单位得到的；开口，对称轴是，当x=时，y有最值，是.抛物线向上直线x=-5-5小0右4向下直线x=44大0（3）将二次函数y=2x2的图像向右平移3个单位后得到函数的图像，其对称轴是，顶点是，当x时，y随x的增大而增大；当x时，y随x的增大而减小.（4）将二次函数y=-3（x-2）2的图像向左平移3个单位后得到函数的图像，其顶点坐标是，对称轴是，当x=时，y有最值，是.y=2（x-3）2直线x=3（3，0）＞3＜3y=-3（x+1）2（-1，0）直线x=-1-1大0(5)抛物线y=4（x-3）2的开口方向，对称轴是，顶点坐标是，抛物线有最点，当x=时，y有最值，其值为抛物线与x轴交点坐标，与y轴交点坐标。向上直线x=3（3，0）低3小0（3，0）（0，36）2)1(43xy2)3(43xy2)5(43xy2)1(43xy如何平移：抛物线开口方向对称轴顶点坐标y=2(x+3)2y=-3(x-1)2y=-4(x-3)2向上直线x=-3(-3,0)直线x=1直线x=3向下向下(1,0)(3,0)不画图指出填空2、按下列要求求出二次函数的解析式：（1）已知抛物线y=a(x-h)2经过点（-3，2）（-1，0）求该抛物线线的解析式.（2）形状与y=-2(x+3)2的图象形状相同，但开口方向不同，顶点坐标是（1，0）的抛物线解析式.（3）已知二次函数图像的顶点在x轴上，且图像经过点（2，-2）与（-1，-8）。求此函数解析式.3.抛物线y=ax2+k有如下特点:当a>0时,开口向上;当a<0时,开口向上.(2)对称轴是y轴;(3)顶点是(0,k).抛物线y=a(x+h)2有如下特点:(1)当a>0时,开口向上,当a<0时,开口向上;(2)对称轴是x=-h;(3)顶点是(-h,0).2.抛物线y=ax2+k可以由抛物线y=ax2向上或向下平移|k|得到.抛物线y=a(x+h)2可以由抛物线y=ax2向左或向右平移|h|得到.(k>0,向上平移;k<0向下平移.)(h>0,向左平移;h<0向右平移.)1.抛物线y=ax2+k、抛物线y=a(x+h)2和抛物线y=ax2的形状完全相同,开口方向一致;(1)当a>0时,开口向上,当a<0时,开口向下;