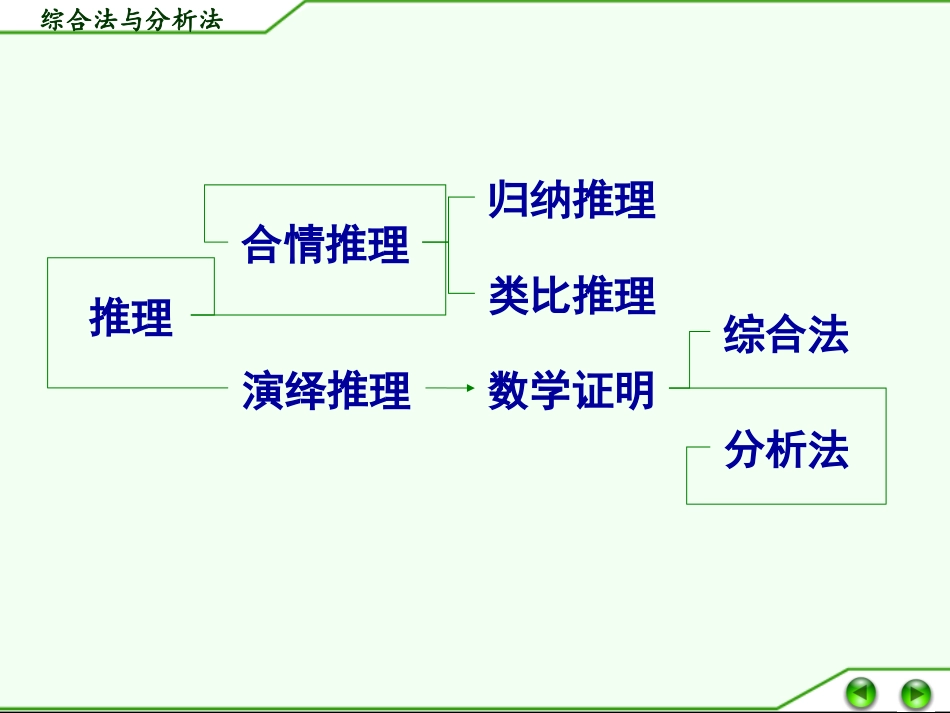
第三章推理与证明─综合法与分析法刘贤建北师大版数学选修1-2综合法与分析法推理合情推理演绎推理归纳推理类比推理数学证明综合法分析法综合法与分析法例1.设a,b都是正实数,求证:abbaab2证明1:因为0,0ba所以.2abba所以abba211两边同乘2ab:即ababbaab222abbaab2证明2:要证只需证只需证只需证只需证由于,所以上式显然成立02baabbaab2abbaab22abbaba222424baababbaab24220222abba即综合法与分析法例1.设a,b都是正实数,求证:abbaab2证明1:因为0,0ba所以.2abba所以abba211两边同乘2ab:即ababbaab222abbaab2结论条件P1P2...综合法与分析法例1.设a,b都是正实数,求证:abbaab2证明2:要证只需证只需证只需证只需证由于,所以上式显然成立02baabbaab2abbaab22abbaba222424baababbaab24220222abba即结论条件、已知P1P2...综合法与分析法综合法:从命题的条件出发,利用定义、公理、定理及运算法则等,通过演绎推理,一步一步地接近要证明的结论,直到完成命题的证明的思维方法。分析法:从求证的结论出发,一步一步地探索保证前一个结论成立的充分条件,直到归结为这个命题的条件,或者归结为定义、公理、定理等的证明的思维方法。综合法与分析法例2.设a,b是实数,求证:)(2222baba证明:因为.222abba所以.222222abbaba即.2222baba即.21222baba所以.2222baba综合法与分析法例3.设a≥3,求证:321aaaa故原不等式成立证明:要证321aaaa即)1)(2(3aaaa只需证123aaaa只需证22123aaaa只需证22)1)(2(3aaaa即)1)(2(3aaaa即23322aaaa此式显然成立即20综合法与分析法练习:请用综合法或分析法证明下列问题1.已知正数x,y满足:x+y=1,求证:411yx2.求证:2325综合法与分析法综合法思维特点:由因导果,从“已知”看“可知”,逐步推向“未知”,其逐步推理,实际是寻找它的必要条件.分析法思维特点:执果索因,从“未知”看“需知”,逐步推向“已知”,其逐步推理,实际是寻找它的充分条件.QQn1QP32QQ21QQQ结论32PP21PP1PQQ结论明显成立的条件(P表示已知条件、已有的定义、定理、公理等,Q表示要证明的结论)综合法与分析法已知(条件)结论nQ2Q1Q......nP2P1P......综合法与分析法ABCEFHG例4.如图,已知BE,CF分别是△ABC的边AC,AB上的高,G为EF的中点,H为BC的中点.求证:HG⊥EF综合法与分析法综合法与分析法综合法与分析法综合法与分析法综合法与分析法综合法与分析法综合法与分析法综合法与分析法综合法与分析法例1.(韦达定理)已知x1和x2是一元二次方程ax2+bx+c=0(a≠0,b2-4ac≥0)的两个根,求证:x1+x2=,x1x2=.abac证明:由于x1和x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,根据球根公式,有abaacbbaacbbxx24242221所以.444)4(242422222221acaacaacbbaacbbaacbbxx综合法与分析法综合法与分析法例1.设a,b都是非负实数,求证:)(2222baba证明1:因为.222abba所以.222222abbaba即.2222baba即.21222baba所以.2222baba证明2:要证)(2222baba只需证222)(21baba即abbaba22222121即0212122abba即0212ba由于,所以上式显然成立02ba