正弦函数变化1VIP免费

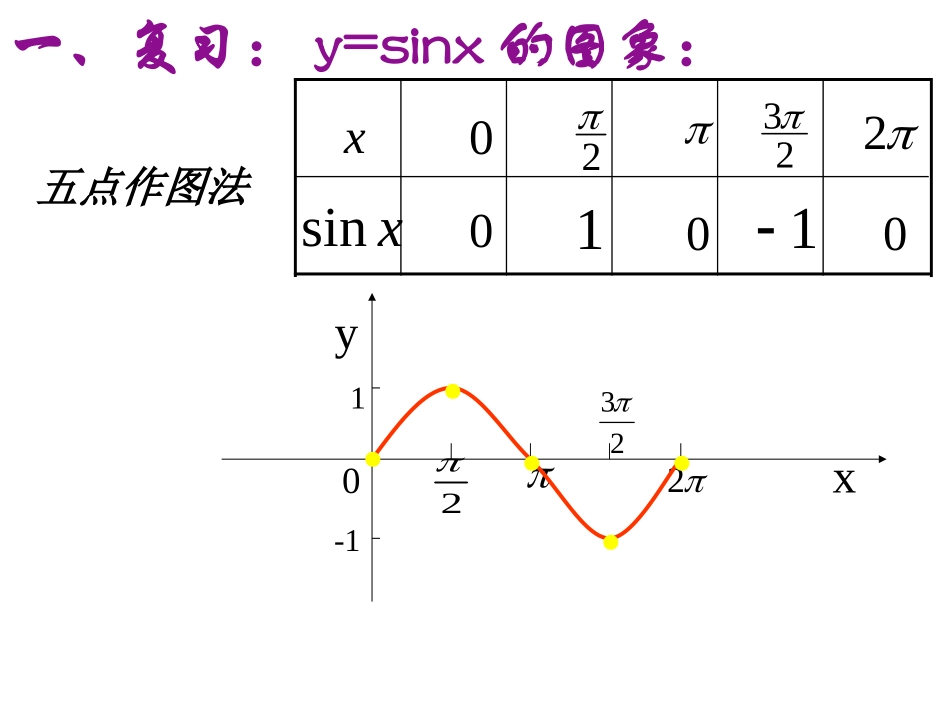
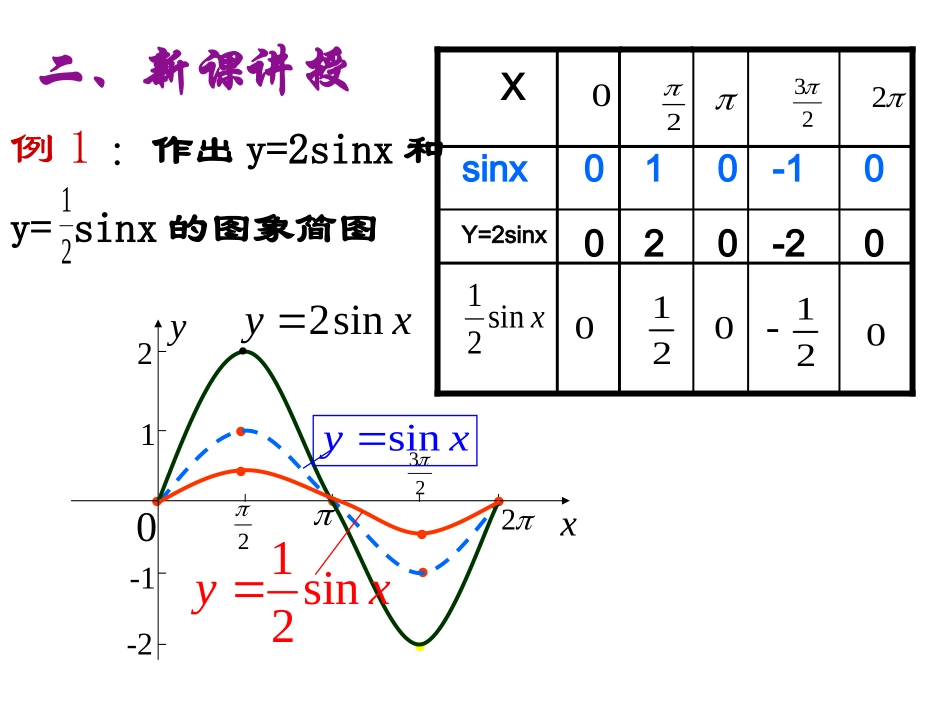
1.5正弦型函数yxANAOZ'ZYXO-2-121-33AYAZ的图象一、复习：y=sinx的图象：022321-1xy.....0223201010五点作图法xsinx........xy022231-12-22sinyx1sin2yxsinyx二、新课讲授例1：作出y=2sinx和y=sinx的图象简图210-2020Y=2sinx0-1010sinxx02322xsin210120120纵坐标伸长到原来的2倍横坐标不变y=sinxy=2sinxy=sinx横坐标不变纵坐标缩短到原来的y=sinx2121xy022231-12-2xysin21sin2yxsinyx当A>1时，将y=sinx图象上所有点的纵坐标伸长到原来的A倍（横坐标不变）当00)与y=sinx的图象A—振幅0xy4222331-1...........0-10100022322342xx2sinx0-1010002324243x2xx2sin2例2：作出和2sinxyxy2sin的简图1sin2yxxy2sin21横坐标伸长到原来的2倍纵坐标不变y=sinxy=sinx纵坐标不变横坐标缩短到原来的y=sinxy=sin2x21xy4222331-1.0xy21sinxy2sin04222331-1xy2T---周期当ω>1时，将y=sinx图象上所有点横坐标缩短为原来的倍（纵坐标不变）；当0<ω<1时,将y=sinx图象上所有点横坐标伸长为原来的倍（纵坐标不变）.11xy21sinxy2sin2、函数y=sinx与y=sinx的图象周期变换.SWF3、函数与的图象)sin(xyxysin例3:作出)4sin(,3sin(xyxy）的简图)sin(xy的图象是将y=sinx的图象沿x轴平移个单位分析：相位变换.SWF253234xy01194sin()yx叫做函数的初相例4.用“五点法”画出函数y=3sin(2x+π/3)的简图.解:651273126x2232032x3sin(2x+π/3)030-30-3ox222312-1-23y63π12综合变换一.gsp综合变换二.gsp方法一例4：画出函数的简图)32sin(3xy3sin(2)3yx方法二）3sin(xy）32sin(xy)]6(2sin[xyxy2sinxysinxysin向左平移个单位3横坐标缩短21横坐标缩短21向左平移个单位6纵坐标伸长3倍sinsinyAxyx4、函数（）与的图象的关系sinsin()yxyx1、若先平移再伸缩，则平移的单位：2、若先伸缩再平移，则平移的单位：先平移变化，再周期变化,最后振幅变化)sin(xy)sin(xy平移个单位横坐标变为原来的倍1xysin)sin(xAy纵坐标变为原来的A倍sin()yAx函数的图象可以看作：方法一先周期变化，再平移变化，最后振幅变化：xysinxysin横坐标变为原来的倍1平移个单位xysin)sin(xAy纵坐标变为原来的A倍方法二sin()yAx函数的图象也可以看作：四、课堂练习的初相是多少？、的周期是多少？、的振幅是多少？、)12sin(432sin3sin812xyxyxy12381多少？），则函数的解析式为，过（，图象，周期为已知该函数的最小值为函数20322)20,0,0(),sin(.5AxAy)473sin(2)453sin(2xyxy或0xy1241251271292121画出函数的简图)43sin(21yxAnswer:sin(),2yAxA1、在函数中叫做振幅；是这个函数的周期；叫做初相。3.1sinsin()sin()yxyxyx（）(2)sinsinsin()yxyxyx2.(1)sinsinyxyAx振幅变换(2)sinsinyxyx周期变换(3)sinsin()yxyx相位变换三、课堂小结