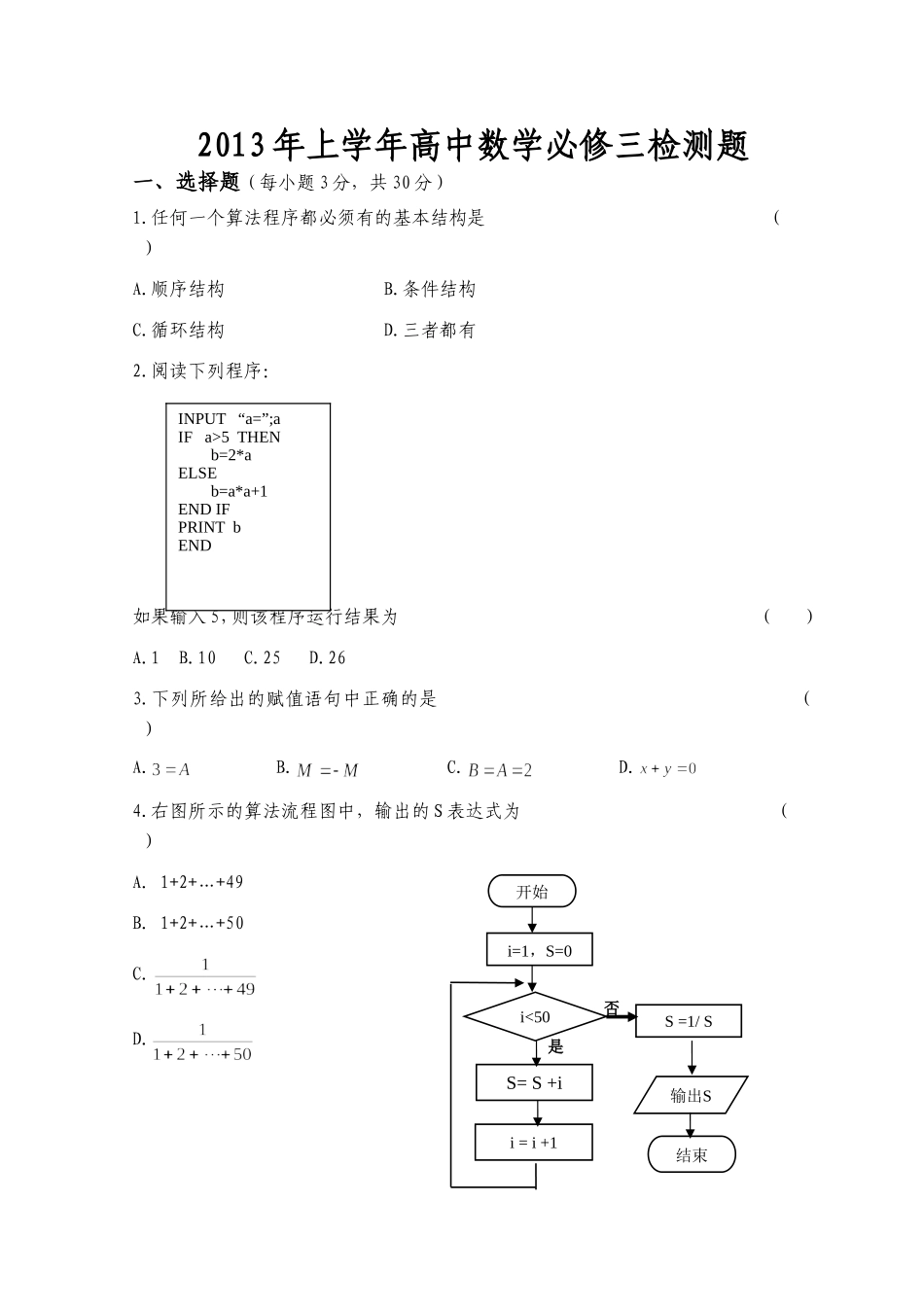
开始i=1,S=0i<50S=S+ii=i+1输出S结束否是S=1/S2013年上学年高中数学必修三检测题一、选择题(每小题3分,共30分)1.任何一个算法程序都必须有的基本结构是()A.顺序结构B.条件结构C.循环结构D.三者都有2.阅读下列程序:如果输入5,则该程序运行结果为()A.1B.10C.25D.263.下列所给出的赋值语句中正确的是()A.B.C.D.4.右图所示的算法流程图中,输出的S表达式为()A.1+2+…+49B.1+2+…+50C.D.INPUT“a=”;aIFa>5THENb=2*aELSEb=a*a+1ENDIFPRINTbEND5.给出如下四对事件:()①某人射击1次,“射中7环”与“射中8环”;②甲、乙两人各射击1次,“甲射中7环”与“乙射中8环”;③甲、乙两人各射击1次,“两人均射中目标”与“两人均没有射中目标”;④甲、乙两人各射击1次,“至少有1人射中目标”与“甲射中,但乙未射中目标”.其中属于互斥事件的有()A.1对B.2对C.3对D.4对6.从某批零件中抽取50个,然后再从50个中抽出40个进行检查,发现合格品有36个,则该批产品的合格率为()A.36%B.72%C.90%D.25%7.我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为()A.45,75,15B.45,45,45C.30,90,15D.45,60,308.甲乙两人下棋,甲获胜的概率为40%,甲不输的概率为90%,则甲乙两人和棋的概率为()A.60%B.30%C.10%D.50%9.取一根长度为3m的绳子拉直后在任意位置剪断,则剪断后两段绳子的长度均不小于1m的概率为()A.B.C.D.不能确定10.对一组数据(i=1,2,...,n),如果将它们改变为(i=1,2,...,n),其中,则下面结论中正确的是()A.平均数与方差均不变B.平均数变了,而方差保持不变C.平均数不变,方差变了D.平均数与方差均发生了变化二、填空题(每小题3分,共15分)11.若六进制数3m502(6),化为十进制数为4934,则m=12.已知与之间的一组数据为则与的回归直线方程必过定点13.从1,2,3,4,5,6这6个数字中,任取2个数字相加,其中为偶数的概率为.14.将一枚硬币连续抛掷3次,正面恰好出现两次的概率为.15.某射手射击一次击中10环,9环,8环的概率分别为,则他射击一次不够8环的概率为三、解答题(55分)16.(10分)某射手在一次射击中射中10环、9环、8环、7环,7环以下的概率分别为0.24,0.28,0.19,0.16,0.13,计算这个射手在一次射击中,(1)射中10环或9环的概率(2)至少射中7环的概率(3)射中环数不是8环的概率?17.(10分)在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:(1)画出频率分布直方图;(2)估计纤度落在[1.38,1.50)中的概率及纤度小于1.40的概率是多少?(3)从频率分布直方图估计出纤度的众数、中位数和平均数0123y135-a7+a分组频数18.(10分)用辗转相除法和更相减损术分别求360,504的最大公约数.19.(10分)用秦九韶算法求多项式当时的值.20.(15分)某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔30分钟抽一包产品,称其重量是否合格,分别记录抽查数据如下:甲车间:102,101,99,98,103,98,99乙车间:110,115,90,85,75,115,110(1)这是什么抽样方法?(2)求出甲、乙两个车间的均值和方差,并说明哪个车间产品较稳定?