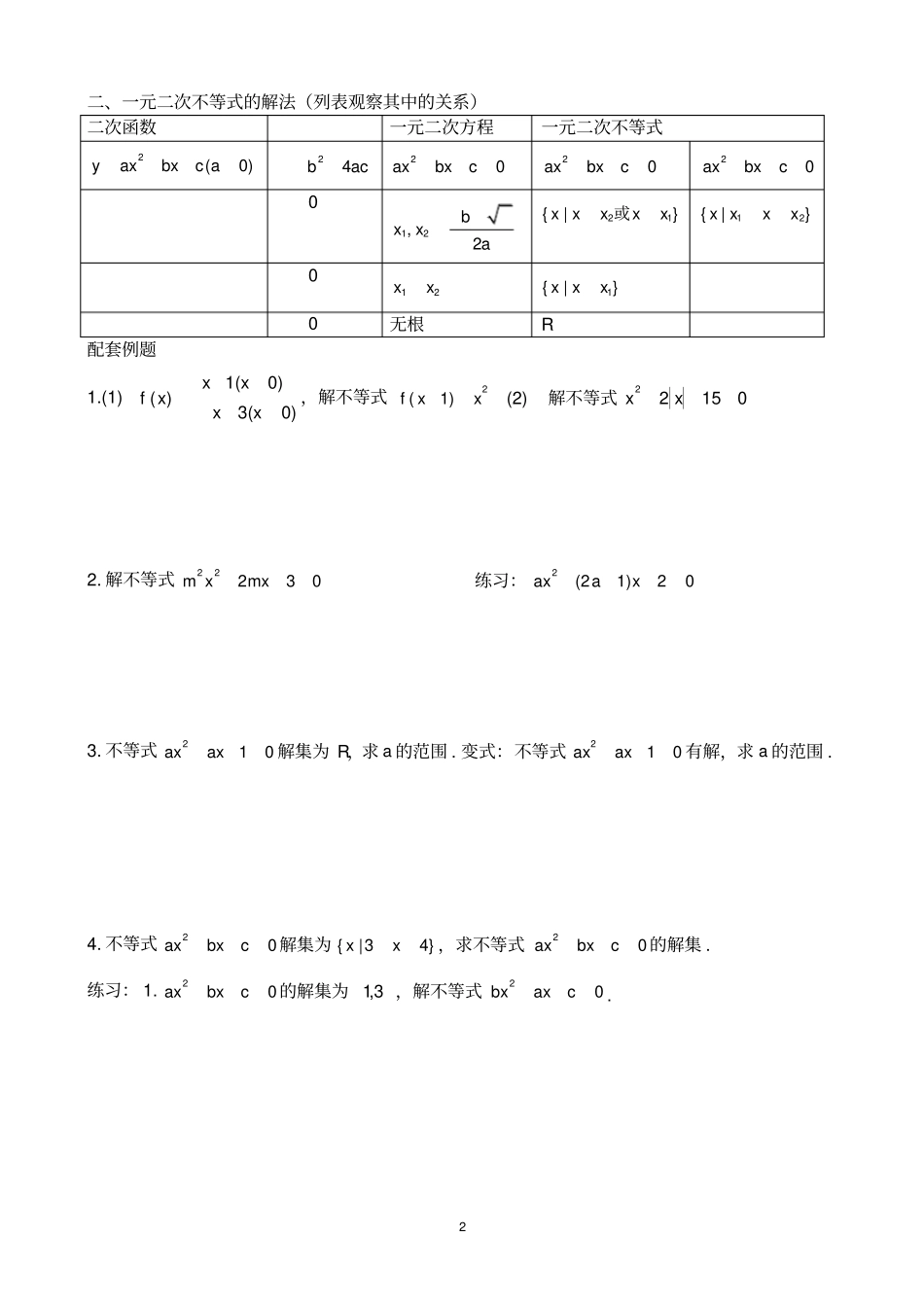
1一元二次不等式、绝对值不等式的解法一、含绝对值不等式的解法1.公式法xaxa0a{|}xxaxa或{|}xaxa0a{|0}xx0aR另:(1)()axbcc或只需把绝对值内看做一个整体(2)()axbcxdcxd或不需要讨论即axbcxdaxbcxd或())cxdaxbcxd或-(2.平方法3.零点分段法(解决含多个绝对值的不等式)4.数形结合法(构造函数作图)5.利用绝对值的几何意义(xax表示数轴上的点到点a的距离)配套例题1.122x2.232xx3.1xx4.25423xxx5.aR,若43xxaR在上恒成立,求a的范围.变式:0a,若43xxaR在上解集非空,求a的范围.变式:12xxaRa在上恒成立,求范围.变式:12xxaRa在上解集非空,求范围.注:第3题可采用平方法以及利用绝对值的几何意义第4题可采用零点分段法以及数形结合法第5题可利用绝对值的几何意义以及数形结合法2二、一元二次不等式的解法(列表观察其中的关系)二次函数一元二次方程一元二次不等式2(0)yaxbxca24bac20axbxc20axbxc20axbxc012,2bxxa21{|}xxxxx或12{|}xxxx012xx1{|}xxx0无根R配套例题1.(1)1(0)()3(0)xxfxxx,解不等式2(1)fxx(2)解不等式22150xx2.解不等式22230mxmx练习:2(21)20axax3.不等式210axax解集为R,求a的范围.变式:不等式210axax有解,求a的范围.4.不等式20axbxc解集为{|34}xx,求不等式20axbxc的解集.练习:1.20axbxc的解集为1,3,解不等式20bxaxc.3含参一元二次不等式的求解策略含参一元二次不等式是同学们学习上的一个难点,为帮助同学们突破这一难点,现介绍几种常用的求解策略。一、利用韦达定理求解例1如果关于x的不等式02cbxax的解集是}|{nxmxx或(m0,即63m时,不等式的解集为3636|mmmxmmmxx或。若0△,即6m时,不等式的解集为32|xx。若0△,即6m时,不等式的解集为R。②当03m即3m时,不等式解集为56xx。③当03m即3m时,0△恒成立,不等式的解集为6633mmmmxxmm。说明:本题的讨论标准分两类,第一类是依据二次项的系数,第二类是依据判别式。三、数形结合,避免讨论例4设集合082|2xxxA,032|2xxxB,089|22aaxxxC,若CBA,求a的取值范围。解:42|xxA,13|xxxB或,41|xxBA,记2289)(aaxxxf,由CBA,知)(xf=0的两根满足4121xx且,由二次函数)(xf的图象得016368)4(0198)1(22aafaaf,解得121a。说明:对于数形结合问题,在熟练的基础上,不用画图,可以在脑海中想象图象的形状,使问题的解决更快捷。