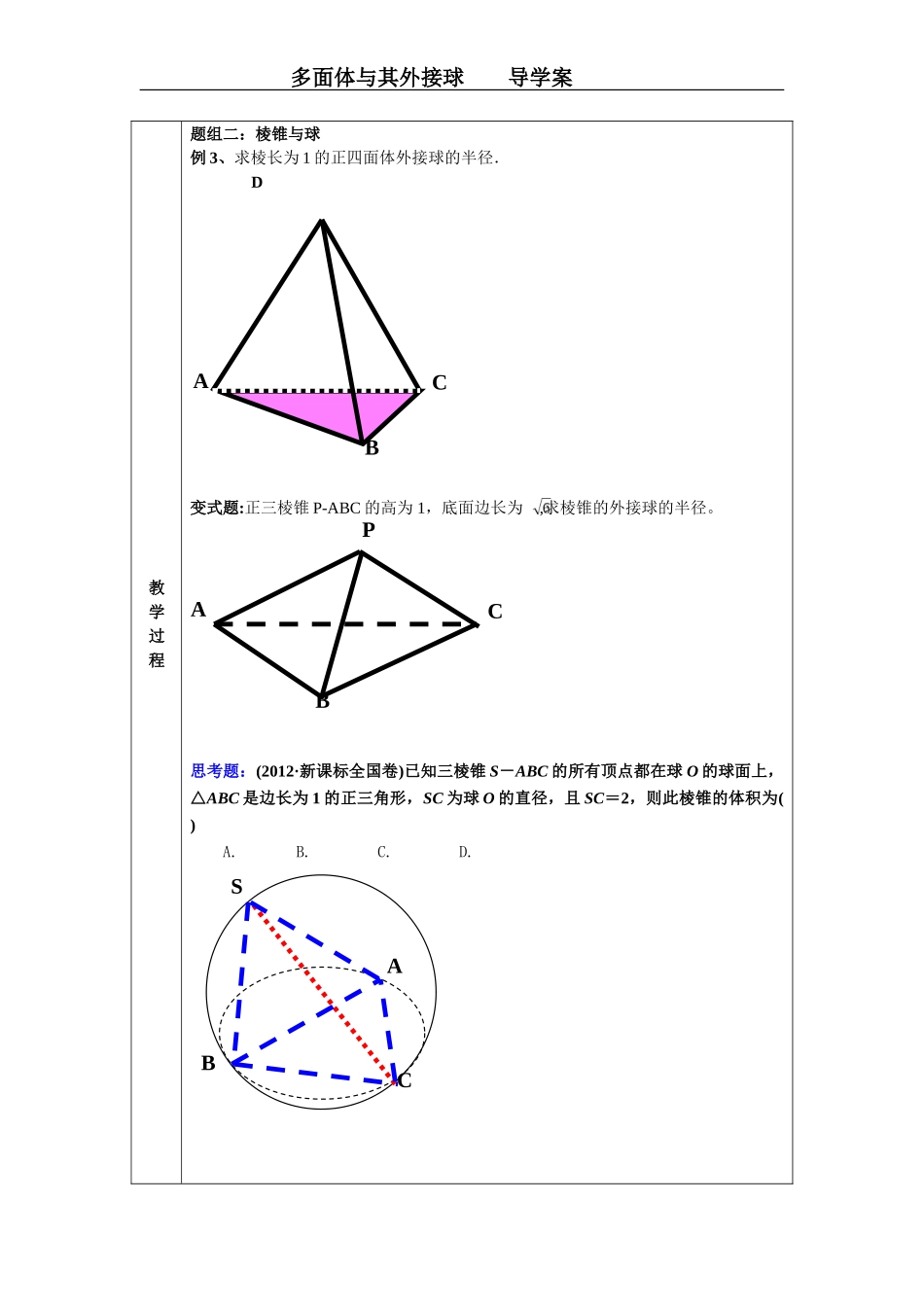
多面体与其外接球导学案教学目标球与多面体的外接多面体与其外接球导学案课前基础一.球的定义1.________以它的直径所在的直线为轴旋转所成的曲面叫做球面.2.________以它的直径所在的直线为轴旋转所成的几何体叫做球体.3.注意:球面和球体的区别:球面仅仅是指球的________;而球体不仅包括球的表面,而且还包括球面所围成的________________。二.球的截面的性质1.用一个平面去截球,截面是_______;用一个平面去截球面,截线是______.2.大圆--截面过______,半径等于球半径;小圆--截面不过______.3.球心和截面圆心的连线_________于截面.4.球心到截面的距离d与球的半径R及截面的半径r的关系:__________________.5.球面上的点P与球直径端点A、B所连三角形为_________三角形三.球的公式球体的体积与表面积______________________,______________________四.多面体与与其外接球1.定义:若一个多面体的__________都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球2.结论:外接球球心到多面体各顶点的距离均________。题组一:棱柱与球例1、若棱长为1的正方体的顶点都在同一球面上,则该球的半径为.例2、设三棱柱的侧棱垂直于底面,AC=CB=AA1=a,∠ACB=90°,顶点都在一个球面上,则该球的半径为ABA1B1C1C多面体与其外接球导学案教学过程题组二:棱锥与球例3、求棱长为1的正四面体外接球的半径.D变式题:正三棱锥P-ABC的高为1,底面边长为,求棱锥的外接球的半径。思考题:(2012·新课标全国卷)已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为()A.B.C.D.CBBCSABCPAA多面体与其外接球导学案