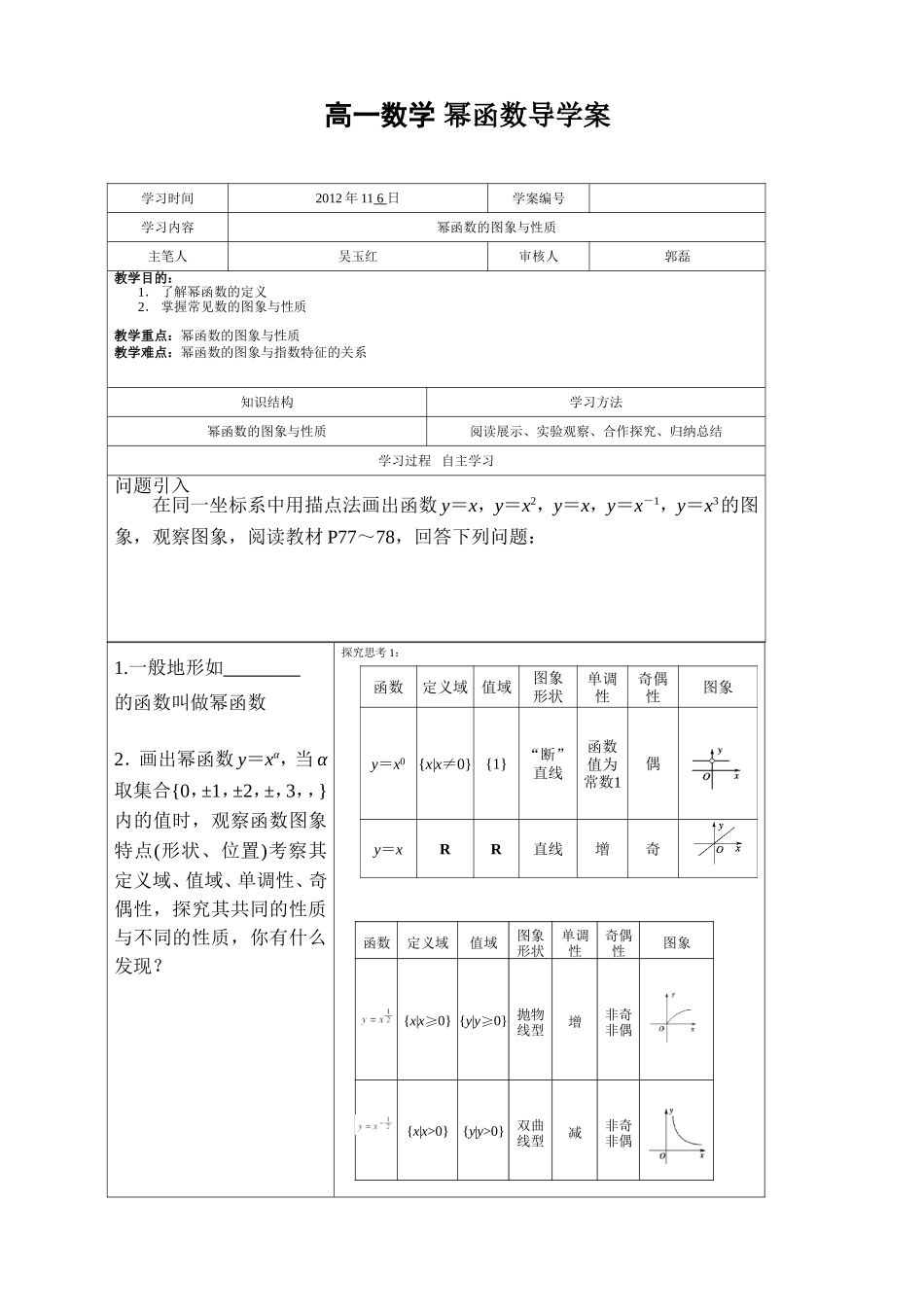
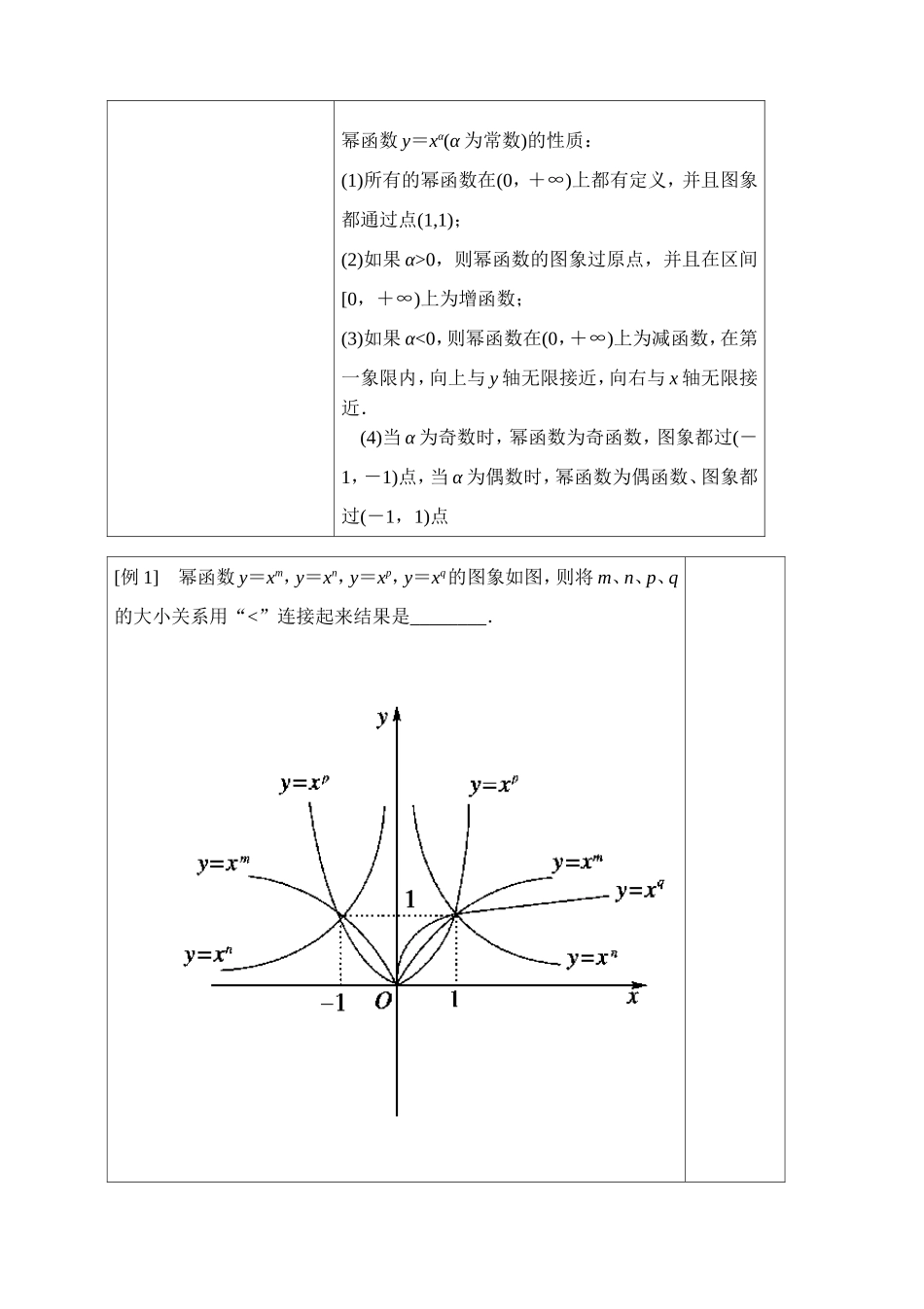
高一数学幂函数导学案1.一般地形如的函数叫做幂函数2.画出幂函数y=xα,当α取集合{0,±1,±2,±,3,,}内的值时,观察函数图象特点(形状、位置)考察其定义域、值域、单调性、奇偶性,探究其共同的性质与不同的性质,你有什么发现?探究思考1:函数定义域值域图象形状单调性奇偶性图象y=x0{x|x≠0}{1}“断”直线函数值为常数1偶y=xRR直线增奇学习时间2012年116日学案编号学习内容幂函数的图象与性质主笔人吴玉红审核人郭磊教学目的:1.了解幂函数的定义2.掌握常见数的图象与性质教学重点:幂函数的图象与性质教学难点:幂函数的图象与指数特征的关系知识结构学习方法幂函数的图象与性质阅读展示、实验观察、合作探究、归纳总结学习过程自主学习问题引入在同一坐标系中用描点法画出函数y=x,y=x2,y=x,y=x-1,y=x3的图象,观察图象,阅读教材P77~78,回答下列问题:函数定义域值域图象形状单调性奇偶性图象{x|x≥0}{y|y≥0}抛物线型增非奇非偶{x|x>0}{y|y>0}双曲线型减非奇非偶幂函数y=xα(α为常数)的性质:(1)所有的幂函数在(0,+∞)上都有定义,并且图象都通过点(1,1);(2)如果α>0,则幂函数的图象过原点,并且在区间[0,+∞)上为增函数;(3)如果α<0,则幂函数在(0,+∞)上为减函数,在第一象限内,向上与y轴无限接近,向右与x轴无限接近.(4)当α为奇数时,幂函数为奇函数,图象都过(-1,-1)点,当α为偶数时,幂函数为偶函数、图象都过(-1,1)点[例1]幂函数y=xm,y=xn,y=xp,y=xq的图象如图,则将m、n、p、q的大小关系用“<”连接起来结果是________.变式训练1.函数y=xa,y=xb,y=xc的图象如图所示,则实数a、b、c的大小关系为()A.c
1,α[分析](1)可利用y=x-的单调性比较,(2)可利用y=x的单调性比较,(3)可利用y=x-的单调性比较,(4)可利用“搭桥法”比较.>0时,aα>1;00时01,α<0时01;第三步,构造幂函数应用幂函数单调性,特别注意含字母时,要注意底数不在同一单调区间内的情形.2.给定一组数值,比较大小的步骤.第一步:区分正负.一种情形是幂函数或指数函数值即幂式确定符号;另一种情形是对数式确定符号,要根据各自的性质进行.第二步:正数通常还要区分大于1还是小于1.第三步:同底的幂,用指数函数单调性;同指数的幂用幂函数单调性;同底的对数用对数函数单调性.变式训练2比较大小:(1)(a+1)1.5,a1.5(a>0);(2)(2+a2)-,2-.[例3]幂函数y=(m2-m-1)xm2-2m-3当x∈(0,+∞)时为减函数,求实数m的值.[解析]∵y=(m2-m-1)xm2-2m-3为幂函数,∴m2-m-1=1,即(m-2)(m+1)=0,∴m=2,或m=-1.当m=-1时,m2-2m-3=0不满足题意,舍去.当m=2时,m2-2m-3=-3满足题设条件,∴m=2.变式训练3已知幂函数f(x)=xm2-2m-3(m∈Z)为偶函数,且在区间(0,+∞)上是减函数.(1)求函数f(x);(2)比较f(-2)与f(1)的大小.归纳总结1.重点掌握α∈{-1,1,0,2,-2,3,,-,,}时,y=xα的图象特征.2.幂函数的图象变化规律幂函数的图象在第一象限内:当x>1时,逆时针方向指数α逐渐增大,即y=xα中α越大,y=xα的图象越远离x轴靠近y轴,α越小越接近x轴.如