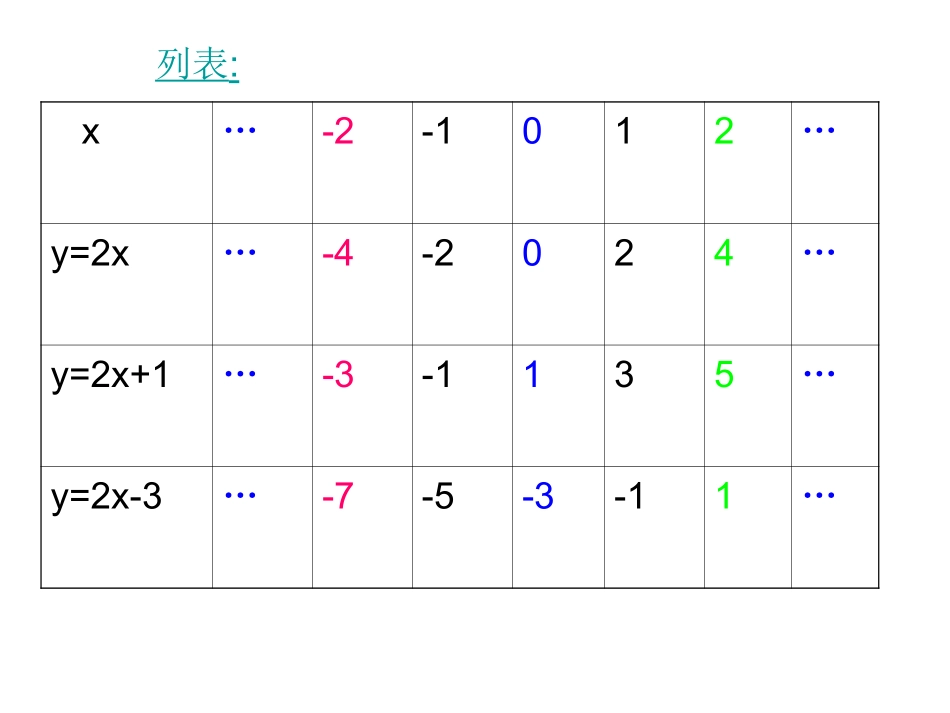
《一次函数的图象和性质》说课稿一、说教材:1、说教材的地位与作用一次函数的图象和性质是正比例函数图象与性质的推广,在许多方面与正比例函数的图象与性质有紧密联系,是本章的重点之一。2、说教学重点:一次函数的图象和性质3、说教学难点:一次函数性质的理解4、说教学目标理解一次函数图象与性质,学会一次函数图象的画法二、说教学思想三、说教法:1、授课时抓住学生已有的知识点,在学生主动参与,教师引导下,使学生更好掌握新知识,对学生进行分类,不同程度的学生采取不同要求。2、采用直观教具和多媒体演示,使学生获得直观印象便于学生理解新知。四、说学法:通过创设不同问题情景,引导不同学生都能积极参与,提高学生分析问题,解决问题的能力。激发学生学习兴趣。五、说教学过程设计:(一)复习引入(5分钟)提问:(1)一次函数的解析式是什么,当b为0时是什么函数?(2)正比例函数的图象与性质怎样?(二)讲授新课(20分钟)1、一次函数的图象与正比例函数图象之间的联系:列表考察正比例函数y=2x分别与一次函数y=2x+1和一次函数y=2x-3的图象之间的关系.引导学生观察,合作探究得出:(10分钟)对于相同的横坐标,(1)一次函数y=2x+1上的点的纵坐标与正比例函数y=2x图象上的点的纵坐标之间的关系;(2)一次函数y=2x-3的图象上的点的纵坐标与正比例函数y=2x图象上的点的纵坐标之间的关系.x…-2-1012…y=2x…-4-2024…y=2x+1…-3-1135…y=2x-3…-7-5-3-11…列表:2、一次函数图象与性质(10分钟)(1)举例:请画出y=x+2和y=x-2的图象。(2)根据图象特征,启发学生联系正比例函数的图象,探究得出一次函数图象的作法:在这条直线上任取两点,过这两点画一条直线即可。(3)学生练习:在同一坐标系内画出y=-2x+3与y=-2x-3的图象3.学生观察,合作探究得出(1)一次函数的图象:一次函数y=kx+b(k,b是常数,k≠0)的图象是过点(0,b)且平行于y=kx的一条直线.把一次函数y=kx+b的图象叫直线y=kx+b(2)根据图形讲解一次函数图象的性质:当k>0时,y的值随着x值的增大而增大;当k<0时,y的值随着x值的增大而减小.(动画展示)(三)知识应用(6分钟)请同学分组合作完成下列问题:自己写出一个一次函数y=kx+b表达式,在平面直角坐标系中描出图象并交流体会一次函数图象的性质.(1)k>0,b>0;(第一、二小组合作完成)(2)k>0,b<0;(第三、四小组合作完成)(3)k<0,b>0;(第五、六小组合作完成)(4)k<0,b<0.(第七、八小组合作完成)(四)巩固练习(5分钟)课本163页练习题(进一步巩固所学新知)(五)学生合作交流小结:(7分钟)1、一次函数图象的特点2、一次函数图象的作法3、一次函数图象的性质(调动学生的积极性对所学知识全面小结,使其成为一个体系,帮助学生全面掌握知识.)(六)作业(2分钟)1、复习本节内容2、作业本上做习题6.42题,3题,4题3、预习下一节内容(巩固所学知识培养良好学习习惯)(七)说板书设计:一次函数的图象正比例函数的图象正比例函数y=kx(k是常数,k≠0)的图象是过点(0,0)的一条直线.一次函数y=kx+b(k,b是常数,k≠0)的图象是过点(0,b)且平行于y=kx的一条直线.yxoy=kxyxoy=kx+b(0,b)正比例函数图象的性质一次函数的图象的性质(1)当k>0时,y的值随着x值的增大而增大;(2)当k<0时,y的值随着x值的增大而减小(1)当k>0时,y的值随着x值的增大而增大;(2)当k<0时,y的值随着x值的增大而减小y=kxxyo(k>0)(k<0)(k>0,b<0)xyy=kx+b(k>0,b>0)o(0,b)xyo(0,b)y=kx+b(k<0,b>0)xyo(0,b)y=kx+b(k<0,b<0)