2.1等差数列VIP免费

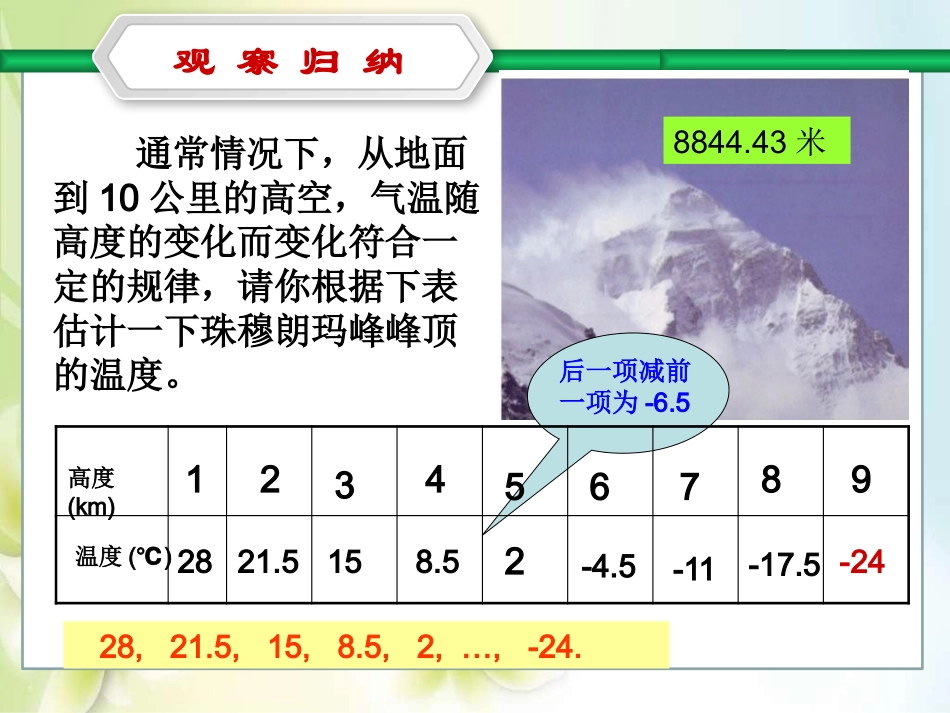
北师大版必修五第一章第二节赣州市厚德外国语学校唐小兰等差数列第一课时观察归纳1896年，雅典举行第一届现代奥运会，到2008年的北京奥运会已经是第29届奥运会。把奥运会举行的年份写下来：1896，1900，1904，…，2008，2012（）你能预测出第31届奥运会的时间吗？2016后一项减前一项为4观察归纳通常情况下，从地面到10公里的高空，气温随高度的变化而变化符合一定的规律，请你根据下表估计一下珠穆朗玛峰峰顶的温度。8844.43米28,21.5,15,8.5,2,…,-24.后一项减前一项为-6.5高度(km)温度()℃1232821.5157-11458.526-4.59-248-17.5（1）1896，1900，1904，…，2008，2012请问：它们有什么共同特点？（2）28,21.5,15,8.5,2,…,-24（3）1，1，1，1，···.共同特点：从第2项起，每一项与它的前一项的差等于同一个常数。定义：如果一个数列从第2项起，每一项与它的前一项的差都等于同一个常数，那么这个数列就叫做等差数列.这个常数叫做等差数列的公差，公差通常用d表示.d=4d=-6.5d=01,(,2)nnaadnNn1,()nnaadnN或用式子表示：观察归纳(1)4，7，10，13，16，…(2)31，25，19，13，7，…(3)0，0，0，0，0，…(4)a，a-b，a-2b，a-3b，…(a、b为常数)(5)1，2，5，8，11，…131,6ad10,0ad1,aadb√√√√14,3ad例1典型例题典型例题等差数列定义的理解(1)注意定义中“从第2项起”这一前提条件的两层含义，其一，第1项前面没有项，无法与后续条件中“与前一项的差”相吻合；其二，定义中包括首项这一基本量，且必须从第2项起保证使数列中各项均与其前面一项作差．(2)注意定义中“每一项与它的前一项的差”这一运算要求，它的含义也有两个：其一是强调作差的顺序，即后面的项减前面的项；其二是强调这两项必须相邻．(3)注意定义中的“同一常数”这一要求，否则这个数列不能称为等差数列．(4)dR等差数列的通项公式daa12daa12daa233addada12da21daa344ada3da31nadna)1(1.)1(1dnaan归纳得:观察-归纳-猜想等差数列{an}的首项为a1，公差为d，求an（迭代法）21aad32aad43aad12nnaad1nnaad….)1(1dnaan共n-1个式子213243-1-2-1---...--nnnnaaaaaaaaaa(1)nd1naa(1)nd通项公式：累加法等差数列的通项公式等差数列通项公式中，知道其中的任意三个量，就可以求出另一个量，即知三求一.通项公式与方程有四个量ɑ1,d,n,ɑn,也就是说，在数列计算题中要注意运用方程思想。1(1)naand巩固训练(1)求等差数列8，5，2，…，的第20项。解：49)3()120(820a(2)等差数列-5，-9，-13，…，的第几项是–401？解：,401,4)5(9,51nada因此，)4()1(5401n解得100ndnaan)1(1,20,385,81=-=-==ndaQ典型例题在等差数列中,已知a5=10,a12=31,求首项a1与公差d.解：由题意可知即这个等差数列的首项是-２，公差是３.解得：说明：由此可以看到：已知等差数列的两项就可以确定这个数列.114101131adad123ad例2巩固训练练习．在等差数列{an}中，(1)已知a1＝2，d＝3，n＝10，则an＝___；(2)已知a1＝3，d＝2，an＝21，则n＝___；(3)已知a1＝12，a6＝27，则d＝___；(4)已知d＝－13，a7＝8，则a1＝___.2910310想一想111(1)(),.,(,).()=0nnaanddnadnNnapnqpdqadpd从函数角度看，因而等差数列的通项公式可以看作是关于的一次式。所以，其也可以表示为：要注意的是，或时，数列是常数数列，对应函数是常数函数。,,nnaapnqpq那么，反过来，如果一个数列｛｝的通项为是常数，那它是等差数列吗？典型例题例3.已知数列{an}的通项公式是an=pn+q，p,q是常数，求证：{an}为等差数列；1.数列{an}为等差数列an=pn+qp、q是常数.解：111,.,(1),.(1),.{}nnnnnnnnNpnqpnqnNpnqpnqpnNnaaaaaaa取数列中的任意相邻两项与它是一个与无关的常数。所以是等差数列。说明：2.证明数列是等差数列的又一常用方法等差数...