二次函数y=a(x+h)2性质VIP免费

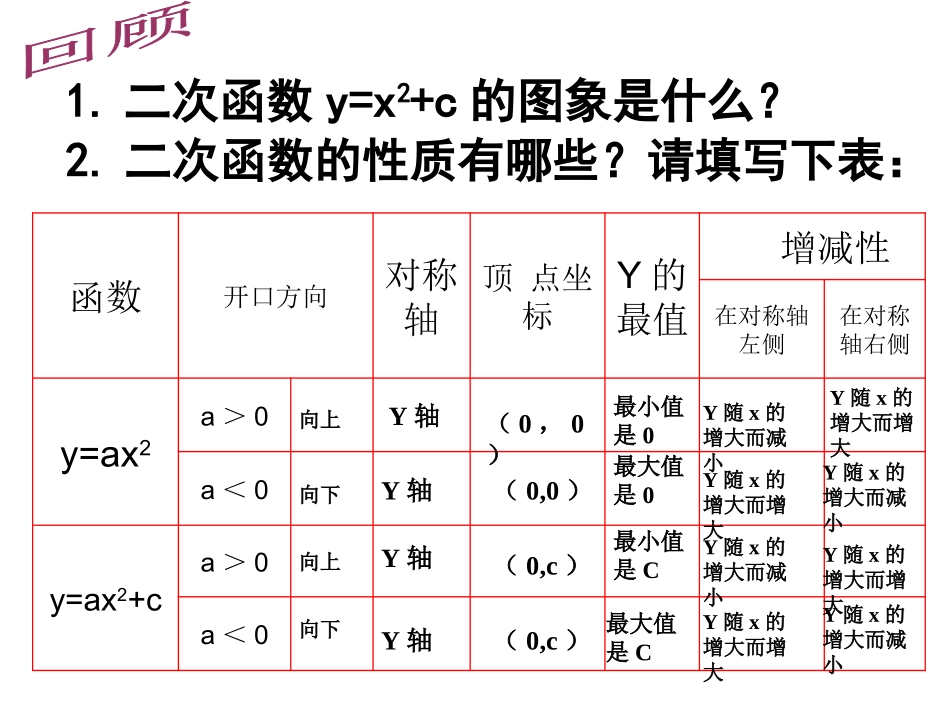
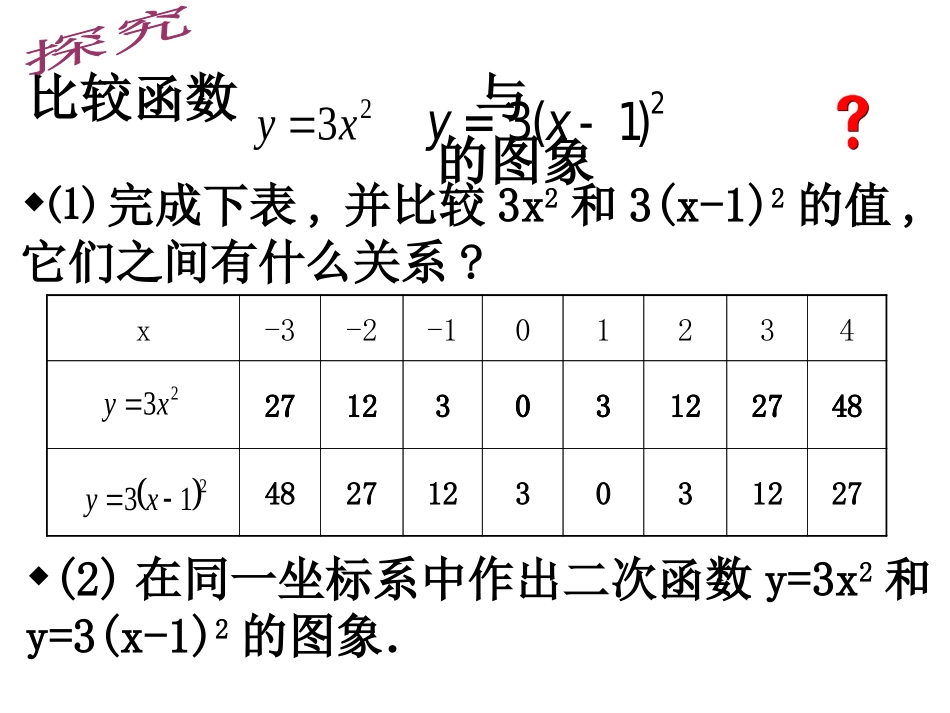
二次函数y=a(x-h)2的图象和性质1.二次函数y=x2+c的图象是什么？2.二次函数的性质有哪些？请填写下表：函数开口方向对称轴顶点坐标Y的最值增减性在对称轴左侧在对称轴右侧y=ax2a＞0a＜0y=ax2+ca＞0a＜0向上Y轴（0，0）最小值是0Y随x的增大而减小Y随x的增大而增大向下Y轴（0,0）最大值是0Y随x的增大而增大Y随x的增大而减小向上Y轴（0,c）最小值是CY随x的增大而减小Y随x的增大而增大向下Y轴（0,c）最大值是CY随x的增大而增大Y随x的增大而减小比较函数与的图象(2)在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象．⑴完成下表,并比较3x2和3(x-1)2的值,它们之间有什么关系?x-3-2-10123423xy23xy()231yx=-213xy271230312274827123031227484827123031227观察图象,回答问题(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x-1)2的值随x的增大而减少？23xy213xy真知从实践走来1.在上面的坐标系中作出二次函数y=3(x+1)2的图象.它与二次函数y=3x2和y=3(x-1)2的图象有什么关系？2.观察：y=3(x+1)2的图象和性质.23xy213xy小组探究：函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象和性质.213xy23xy213xy213xyy二次函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象二次函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象二次函数y=a(x-h)2的性质开口大小抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x-h)2(a>0)y=a(x-h)2(a<0)（h，0）（h，0）直线x=h直线x=h在x轴的上方(除顶点外)在x轴的下方(除顶点外)向上向下当x=h时,最小值为0.当x=h时,最大值为0.在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.越小,开口越大.越大,开口越小.aa2hxay2axyX=hX=h二次函数y=a(x-h)2与y=ax2的图象形状相同,可以看作是抛物线y=ax2整体沿x轴平移了个单位(当h>0时,向右移个单位;当h<0时,向左移个单位)得到的.hhh函数开口方向对称轴顶点坐标Y的最值增减性在对称轴左侧在对称轴右侧y=ax2a＞0a＜0y=ax2+ca＞0a＜0y=a(x-h)2a＞0a＜0向上Y轴（0，0）最小值是0Y随x的增大而减小Y随x的增大而增大向下Y轴（0，0）最大值是0Y随x的增大而增大Y随x的增大而减小向上Y轴（0，c）最小值是CY随x的增大而减小Y随x的增大而增大向下Y轴（0，c）最大值是CY随x的增大而增大Y随x的增大而减小向上直线x=h（h，0）Y随x的增大而减小最小值是0Y随x的增大而增大向下直线x=h（h，0）最大值是0Y随x的增大而增大Y随x的增大而减小(1)二次函数y=2(x+5)2的图像是,开口,对称轴是,当x=时,y有最值,是.(2)二次函数y=-3(x-4)2的图像是由抛物线y=-3x2向平移个单位得到的;开口,对称轴是,当x=时,y有最值,是.(3)将二次函数y=2x2的图像向右平移3个单位后得到函数的图像,其对称轴是,顶点是,当x时,y随x的增大而增大;当x时,y随x的增大而减小.(4)将二次函数y=-3(x-2)2的图像向左平移3个单位后得到函数的图像,其顶点坐标是,对称轴是,当x=时,y有最值,是.(5)将函数y=3(x-4)2的图象沿x轴对折后得到的函数解析式是；将函数y=3(x-4)2的图象沿y轴对折后得到的函数解析式是.(6)把抛物线y=a(x-4)2向左平移6个单位后得到抛物线y=-3(x-h)2的图象,则a=,h=.若抛物线y=a(x-4)2的顶点A,且与y轴交于点B,抛物线y=-3(x-h)2的顶点是M,则SΔMAB=.(7)将抛物线y=2x2-3先向上平移3单位,就得到函数的图象,在向平移个单位得到函数y=2(x-3)2的图象.(8)函数y=(3x+6)2的图象是由函数.的图象向左平移5个单位得到的;其图象开口向,对称轴是,顶点坐标是,当x时,y随x的增大而增大,当x=时,y有最值是.小结拓展你认为今天这节课最需要掌握的是__________？