二次函数y=a(x-h)2+k的图像与性质.1二次函数图像与性质(4)(公开课)VIP免费

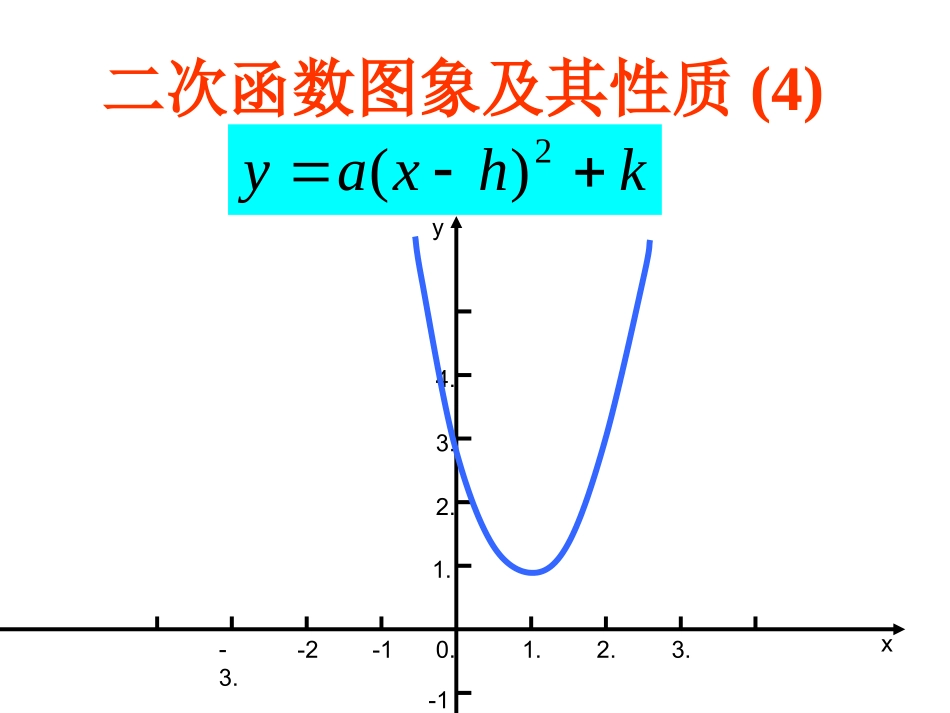
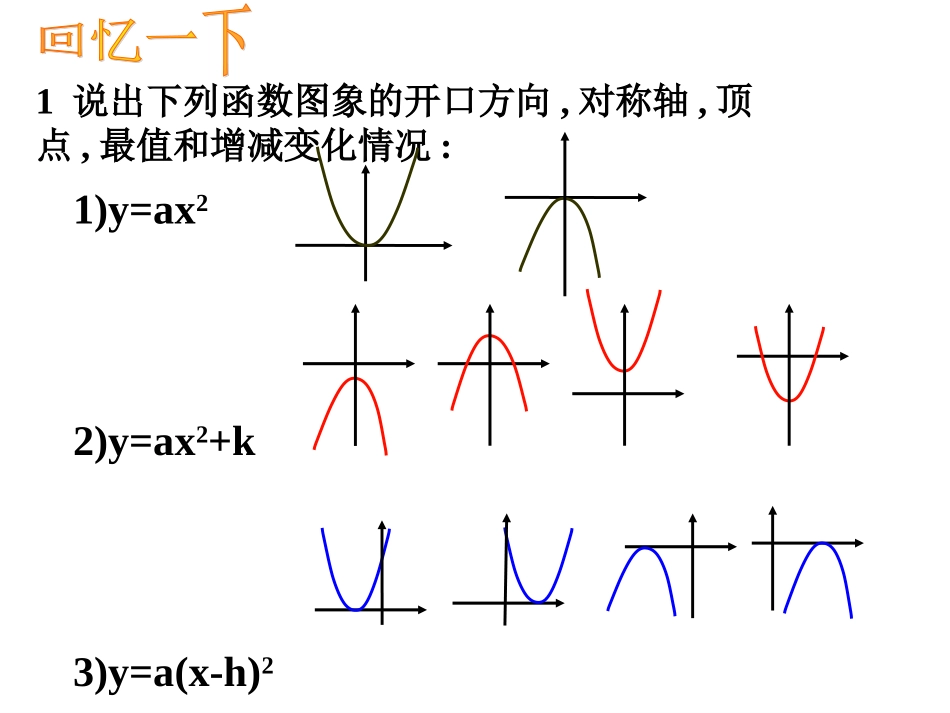
1.2.3.-1-2-3.0.1.2.3.4.-1xy二次函数图象及其性质(4)khxay2)(1说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:1)y=ax22)y=ax2+k3)y=a(x-h)2请说出二次函数y=2x²-3与抛物线y=2(x+3)2如何由y=2x2怎么平移而来的？21y(x1)22xx……-4-4-3-3-2-2-1-1001122……y=-0.5(x+1)y=-0.5(x+1)22-2-2…………21yx221y(x1)22画出函数的图象，指出它的开口方向、对称轴及顶点。抛物线经过怎样的变换可以得到抛物线？-6.5-6.5-4-4-2.5-2.5-2-2-2.5-2.5-4-4-6.5-6.5直线x=-1xyO21y(x1)2221yx221yx2-2探讨1探讨探讨22说说二次函数说说二次函数y=2xy=2x²²,,y=2(x-1)y=2(x-1)²²,y=2x,y=2x²²+1+1，，y=2(x-1)y=2(x-1)²²+1+1图象之间的图象之间的关系？关系？1.2.3.-1-2-3.0.1.2.3.4.-1xy5y=2(x-1)2+1y=2(x-1)2y=2x21.2.3.-1-2-3.0.1.2.3.4.-1xy5y=2(x-1)2+1y=2x2+1y=2x2y=a(x-h)2+ka>0a<0开口方向顶点坐标对称轴增减性极值向上向下(h,k)(h,k)x=hx=h当xh时，y随着x的增大而增大。当xh时，y随着x的增大而减小。x=h时,y最小=kx=h时,y最大=k及时总结及时总结抛物线抛物线y=a(x-h)y=a(x-h)22+k+k可以看作是由抛物线可以看作是由抛物线y=axy=ax22经过平移经过平移得到的。得到的。顶点式练习1:指出下面函数的开口方向，对称轴，顶点坐标，最值。1)y=2(x+3)2+52)y=4(x-3)2+73)y=-3(x-1)2-24)y=-5(x+2)2-6练习2:对称轴是直线x=-2的抛物线是()Ay=-2x2-2By=2x2-2Cy=-1/2(x+2)2-2Dy=-5(x-2)2-6C1.抛物线的顶点为(3,5)此抛物线的解析式可设为()A：y=a(x+3)2+5B：y=a(x-3)2+5C：y=a(x-3)2-5D：y=a(x+3)2-5已知二次函数的图象的顶点为（已知二次函数的图象的顶点为（11，，-4.5-4.5），且经过点），且经过点（－（－22，，00），求该二次函数的函数关系式。），求该二次函数的函数关系式。拓展拓展1)若抛物线y=-x2向左平移2个单位,再向下平移4个单位所得抛物线的解析式是________2)如何将抛物线y=2(x-1)2+3经过平移得到抛物线y=2x23)将抛物线y=2(x-1)2+3经过怎样的平移得到抛物线y=2(x+2)2-1y=a(x-h)2+ka>0a<0开口方向顶点坐标对称轴增减性极值向上向下(h,k)(h,k)x=hx=h当xh时，y随着x的增大而增大。当xh时，y随着x的增大而减小。x=h时,y最小=kx=h时,y最大=k回顾与反思回顾与反思抛物线抛物线y=a(x-h)y=a(x-h)22+k+k可以看作是由抛物线可以看作是由抛物线y=axy=ax22经过平移经过平移得到的。得到的。顶点式作业：作业：P41P41第第55题题