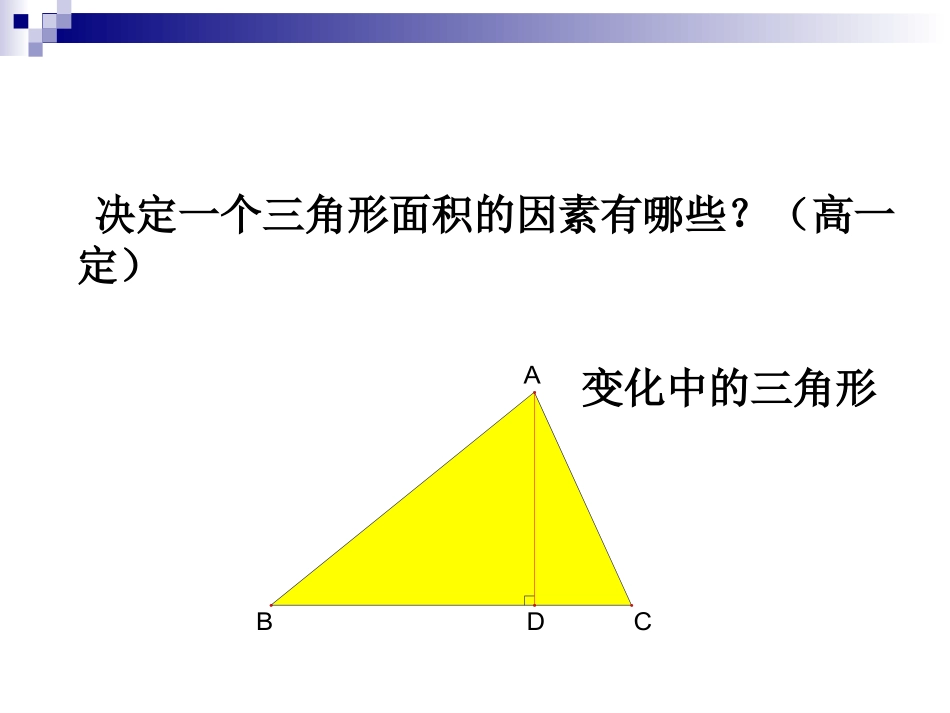
康平县郝官九年一贯制学校刘会练一练练一练婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,6周岁、10周岁时体重分别大约是1周岁时的2倍、3倍.年龄刚出生6个月1周岁2周岁6周岁10周岁体重/千克根据表中的数据,说一说儿童从出生到10周岁之间体重是怎样随着年龄的增长而变化的.(2)某婴儿在出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:(1)上述哪些量在发生变化?自变量和因变量各是什么?发生变化的量是:体重和时间自变量是:因变量是:时间体重3.57.010.514.021.031.5年龄刚出生6个月1周岁2周岁6周岁10周岁体重/千克3.5710.5142131.5决定一个三角形面积的因素有哪些?(高一定)变化中的三角形DBCA想一想想一想ABC如图,⊿ABC底边BC上的高是6厘米.当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?CCSABC⊿=―BC·h=3BC12C(1)在这个变化过程中,自变量、因变量各是什么?(2)如果三角形的底边长为x(厘米),那么三角形的面积y(厘米2)可以表示为y=3x(3)当底边长从12厘米变化到3厘米时,三角形的面积从______厘米2变化到____厘米2369y=3x表示了和之间的关系,它是变量y随x变化的关系式.你能直观地表示这个关系式吗?自变量x关系式y=3x因变量y三角形底边长x面积y注意:关系式是我们表示变量之间的另一种方法,利用关系式,如y=3x,我们可以根据任何一个自变量值求出相应的因变量的值.rh3hrv2做一做做一做1.如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化.4厘米(1)在这个变化过程中,自变量、因变量各是什么?(2)如果圆锥底面半径为r(厘米),那么圆锥的体积v(厘米3)与r的关系式为______________(3)当底面半径由1厘米变化到10厘米时,圆锥的体积由厘米3变化到厘米3.3r4v23434002.如图,圆锥的底面半径是2厘米,当圆锥的高由小到大变化时,圆锥的体积也随之变化。2㎝(1)在这个变化过程中,自变量、因变量各是什么?(2)如果圆锥的高为h(厘米),那么圆锥的体积v(厘米3)与h之间的关系式为.(3)当高由1厘米变化到10厘米时,圆锥的体积由厘米3变化到厘米33h4v34340议一议:你知道什么是“低碳生活”吗?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低碳、特别是二氧化碳的排放量的一种方式.议一议:(1)家居用电的二氧化碳排放量可以用关系式表示为_____________,其中的字母表示________________.议一议:(2)在上述关系式中,耗电量每增加1KW·h,二氧化碳排放量增加___________.当耗电量从1KW·h增加到100KW·h时,二氧化碳排放量从_______增加到________.议一议:(3)小明家本月用电大约110KW·h、天然气20m3、自来水5t、油耗75L,请你计算一下小明家这几项的二氧化碳排放量.随堂练习随堂练习自变量d因变量T1.在地球某地,温度T(C)与高度d(m)的关系可以近似地用来表示,根据这个关系式,当d的值分别是0,200,400,600,800,1000时,计算相应的T值,并用表格表示所得结果.高度d/m02004006008001000温度T/°C10.008.677.336.004.673.33150d-10T150d-10T2.如图所示,梯形上底的长是x,下底的长是15,高是8.(1)梯形面积y与上底长x之间的关系式是什么?(2)用表格表示当x从10变到20时(每次增加1),y的相应值;(3)当x每增加1时,y如何变化?说说你的理由;(4)当x=0时,y等于什么?此时它表示的什么?x8151.本节主要是探索了图形中的变量关系.2.能用关系式表示变量之间的关系.3.能根据关系式求值.