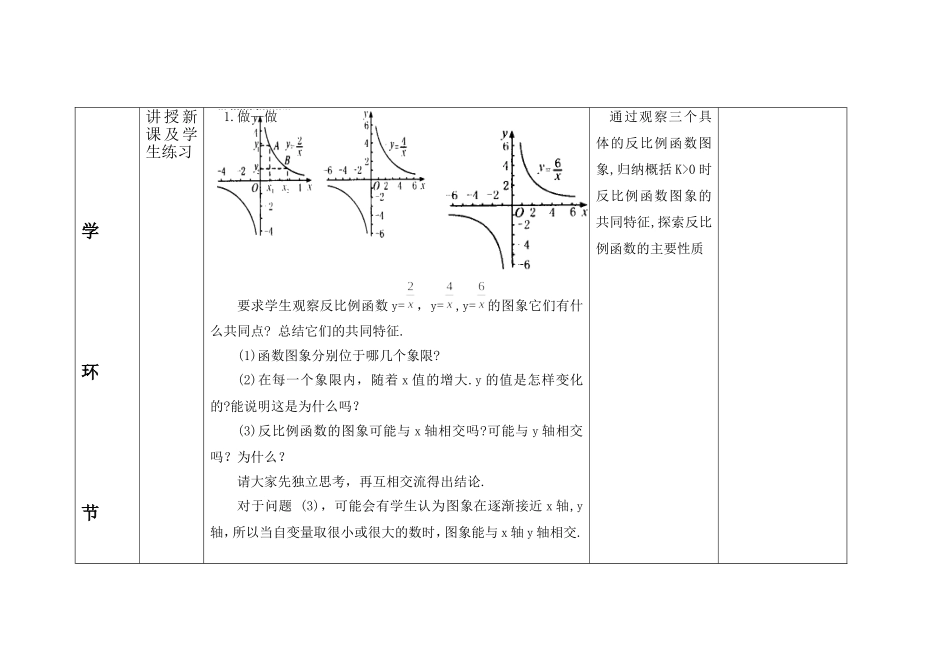
科目数学年级九学期一备课人邓树春课题反比例函数的图象与性质(二)课标要求能画出反比例函数的图像,根据图像和表达式y=k/x探索并理解k>0和k<0时,图像的变化情况。教材分析本节课通过对反比例函数图像的认识,归纳一类图像的性质,进一步理解反比例函数。学情分析学生已经对反比例函数图象的初步认识,并且具有一定的识图能力.通过观察、分析函数的图像,对主要性质作出描述,培养学生获取知识的能力,教学目标1.进一步巩固作反比例函数的图象.2.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质.3、通过画反比例函数图象,从图象中获取信息.对图象性质的研究,训练学生的探索能力和语言组织能力.教学重点通过观察图象,归纳概括反比例函数图象的共同特征,探索反比例函数的主要性质.教学难点从反比例函数的图象中归纳总结反比例函数的主要性质.教学资源教学过程教学内容设计意图再设计导入上节课我们学习了画反比例函数的图象,并通过图象总结出当k>0时,函数图象的两个分支分别位于第一、三象限内;当k<0时,函数图象的两个分支分别位于第二、四象限内.这是从函数的图象位于哪些象限来研究了反比例函数的性质.在学习正比例函数和一次函数图象时,还研究了当k>0时,y的值随x的增大而增大,当k<0时,y的值随x值的增大而减小,即函数值随自变量的变化而变化的情况,以及函数图象与x轴,y轴的交点坐复习上节内容,,并引导学生类比一次函数图象性质引出反比例函数教标.本节课我们来研究一下反比例函数的有关性质.图象其他性质学环节讲授新课及学生练习1.做—做要求学生观察反比例函数y=,y=,y=的图象它们有什么共同点?总结它们的共同特征.(1)函数图象分别位于哪几个象限?(2)在每一个象限内,随着x值的增大.y的值是怎样变化的?能说明这是为什么吗?(3)反比例函数的图象可能与x轴相交吗?可能与y轴相交吗?为什么?请大家先独立思考,再互相交流得出结论.对于问题(3),可能会有学生认为图象在逐渐接近x轴,y轴,所以当自变量取很小或很大的数时,图象能与x轴y轴相交.通过观察三个具体的反比例函数图象,归纳概括K>0时反比例函数图象的共同特征,探索反比例函数的主要性质可以从函数式的定义域、函数与方程等角度进行解释。总结:当k>0时,函数图象分别位于第一、三象限内,并且在每一个象限内,y随x的增大而减小.2.议一议用类推的方法来研究y=-,y=-,y=-的图象有哪些共同特征?通过讨论,可以得出如下结论:反比例函数y=的图象,当k>0时,在每一象限内,y的值随x值的增大而减小;当k<0时,在每一象限内,y的值随x值的增大而增大.例:1、已知函数,当x<0时,函数图象在第象限,y随x的增大而.2、已知反比例函数(k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx-k的图象经过()A、第一、第二、三象限B、第一、二、三象限C、第一、三、四象限D、第二、三、四象限3、若点A(-1,y1),B(2,y2),C(3,y3)都在反比例函数的图象上,则下列关系式正确的是()A、y1<y2<y3B、y2<y1<y3C、y3<y2<y1D、y1<y3<y23.想一想(1)在一个反比例函数图象任取两点P、Q,过点Q分别作x轴,y轴的平行线,与坐标轴围成的矩形面积为S1;过点Q分别作x轴y轴的平行线,与坐标轴围成的矩形面积为S2,S1与S2有什么关系?为什么?学生进一步深入了解其他性质,体(2)将反比例函数的图象绕原点旋转180°后.能与原来的图象重合吗?随堂练习1,2会代数推理的意义.课堂小结本节课学习了如下内容.1.反比例函数y=的图象,当k0时,在第一、三象限内,在每一象限内,y的值随,值的增大而减小;当k