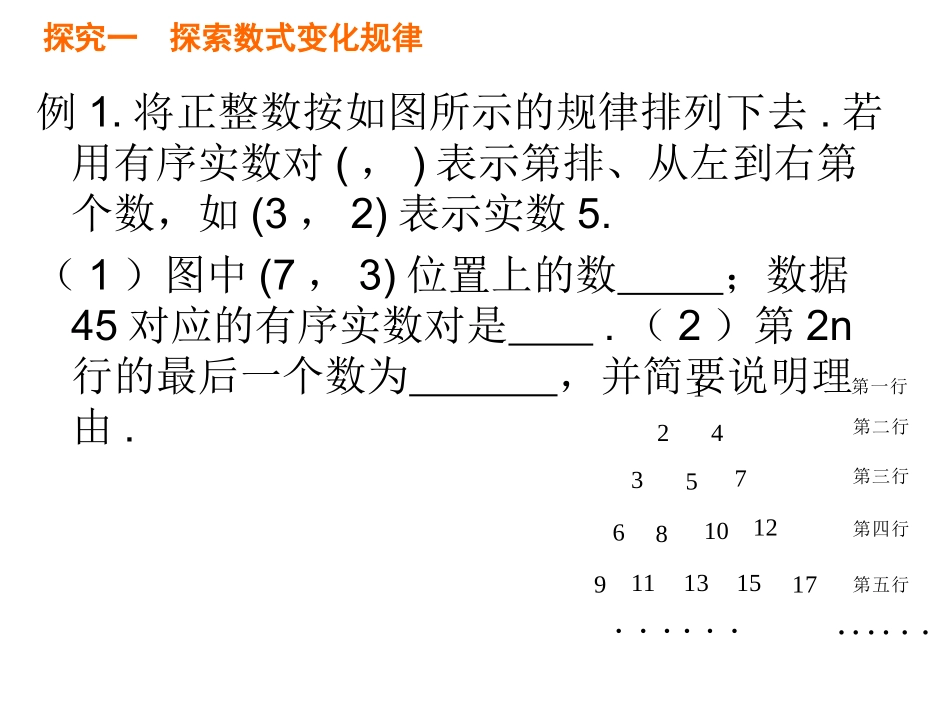
中考复习专题探索规律例1.将正整数按如图所示的规律排列下去.若用有序实数对(,)表示第排、从左到右第个数,如(3,2)表示实数5.(1)图中(7,3)位置上的数;数据45对应的有序实数对是.(2)第2n行的最后一个数为,并简要说明理由.••••••••••••第五行第四行第三行第二行第一行151713121110987654321探究一探索数式变化规律探究一探索数式变化规律例2观察下列等式:①9×0+1=1;②9×1+2=11;③9×2+3=21;④9×3+4=31;(1)请按以上规律写出第5个等式:;(2)请用含字母n的式子表示第n个等式:(3)试说明以上规律的正确性.探究一探索数式变化规律例3、观察下列等式:根据上述规律解决下列问题:(1)完成第四个等式:()﹣()=()(2)写出你猜想的第n个等式(用含n的代数式表示),并证明正确性。41【思路导引】特例→归纳基础归纳概括→在特例基础上,观察、抽象、概括猜想→得出一般性结论运用你得到的结论解决问题探究一探索数式变化规律探究二探索图形变化规律例4、如图,在下列n×n的正方形网格中,请按图形的规律,探索以下问题:(1)第④个图形中阴影部分小正方形的个数为;(2)第个图形中阴影部分小正方形的个数为;(2)是否存在阴影部分小正方形的个数是整个图形中小正方形个数7/9的?如果存在,是第几个图形;如果不存在,请说明理由.探究二探索图形变化规律例5、如图,一个3×2的矩形(即长为3,宽为2)可以用两种不同方式分割成3个或6个边长是正整数的小正方形,即:小正方形的个数最多是6个,最少是3个.(1)一个5×2的矩形用不同的方式分割后,小正方形的个数最多是个,最少是个;(2)一个7×2的矩形用不同的方式分割后,小正方形的个数最多是个,最少是个;(3)一个(2n+1)×2的矩形用不同的方式分割后,小正方形的个数最多是个;最少是个.(n是正整数)【解析】第一个图形:是一个3×2的矩形,最少可分成1+2个正方形,最多可分成3×2个正方形;第二个图形:是一个5×2的矩形,最少可分成2+2个正方形,最多可分成5×2个正方形;第三个图形:是一个7×2的矩形,最少可分成3+2个正方形,最多可分成7×2个正方形;…;第n个图形:是一个(2n+1)×2的矩形,最少可分成n+2个正方形,最多可分成2(2n+1)=4n+2个正方形.【答案】(1)10,4;(2)14,5;(3)4n+2,n+2.探究二探索图形变化规律【思路导引】研究每次图形变化的特征发现图形变化次数确定图形位置根据图形变化次数确定图形位置确定相应图形中的元素特征探究二探索图形变化规律探究三探索数形变化规律例6、如图,在函数y=(x>0)的图象上有点P1,P2,P3,…,Pn,Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成若干个矩形,如图所示,将图中阴影部分的面积从左至右依次记为S1,S2,S3,…,Sn.(1)S1=;(2)求Sn的表达式.(用含n的代数式表示)x8【答案】∵点P1,P2,P3,…,Pn,Pn+1的坐标分别为∴S1,S2,S3,…,Sn分别为探究三探索数形变化规律探究三探索数形变化规律例7、在平面直角坐标系中,△ABC的三个顶点都在边长为1的小正方形的格点上,△ABC关于y轴的对称图形为△ABC,以△ABC与△ABC组成一个基本图形,不断复制与平移这个图形,得到如图所示的图案。(1)观察以上图形并填写下列各点坐标:A(,),A(,),…,A(,)(2)若△ABC是这组图形中的一个三角形,当n=2019时,则m=,k=【思路导引】从“形”的角度分析图形特征从“数”的角度分析数式特征对照并验证结论得到一般规律确定相应图形中的元素特征课堂总结(见安徽历年中考真题汇编第10题、13题)中考真题再现