求一次函数的表达式-(3)VIP免费

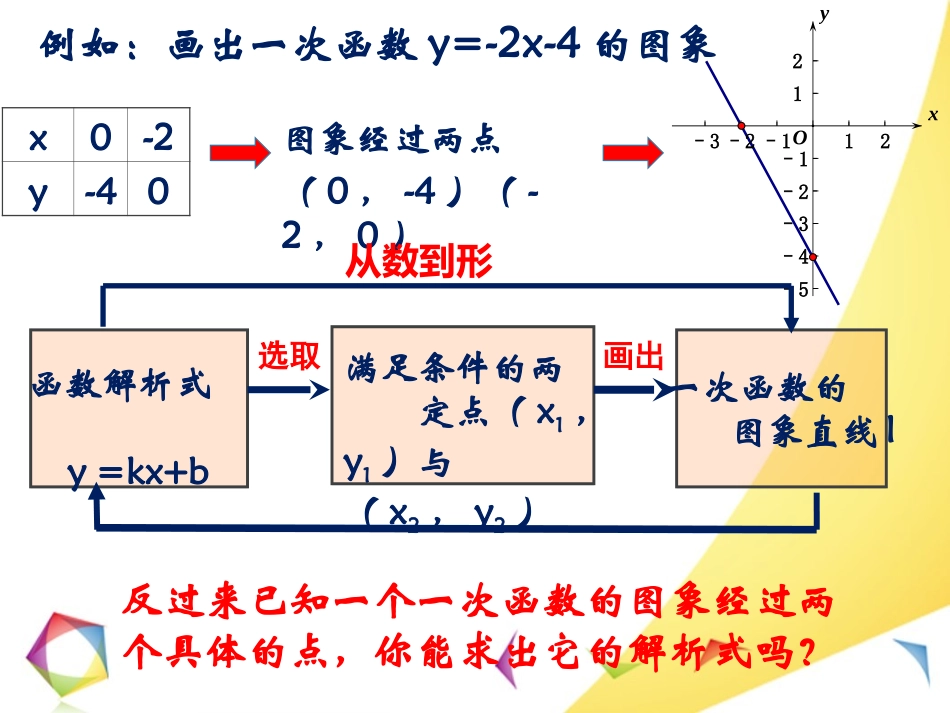
泉州五中董黎芳；一次函数的关系式：______________)1(.0___________k是常数，其中ykxbkb、=(0)ykxk正比例。一次函数的图象是：___________)3(一条直线时，特别地，当0___)2(b函数。叫做_____________________一次函数x0-2y-40例如：画出一次函数y=-2x-4的图象图象经过两点（0，-4）（-2，0）xy–1–2–312–1–2–3–4–512O满足条件的两定点（x1，y1）与（x2，y2）函数解析式y=kx+b一次函数的图象直线l选取画出从数到形反过来已知一个一次函数的图象经过两个具体的点，你能求出它的解析式吗？例1：求这个函数的表达式。，，与点，过点已知一次函数的图象经)51()11(求一次函数y=kx+b的解析式，关键是求出k、b的值。这种先设待求函数解析式（其中含有待定系数），再根据条件确定解析式中未知的系数，从而得出函数解析式的方法，叫做待定系数法求一次函数关系式的一般步骤：（1）设：设出函数关系式y=kx+b（k≠0）（2）代：把已知条件代入关系式，得到关于k和b的方程（组）（3）解：解方程组，求出k和b的值。（4）写：把求出的k和b的值代回y=kx+b,即得所求的函数关系式。例2：已知)1(，时，且当61yx.___________的函数关系式是与则xyy=kx（k≠0）∴k·(-1)=-6∴k=6y=6x成正比例，与xy._____________1031)2(的函数关系式是与；则时，成正比例关系，且当与已知xyyxxy解：设y-1=kx（k≠0）∴依题意：3·k=10-1∴k=3y=3x+1设练习：问题：的表达式；并回答以下求出直线是原点；两点，、轴于轴、直线分别交的图象如图所示，：已知直线lyxkbkxylOBA)0(所对应的函数表达式。求平移后的直线，点的图象平移，使它经过将直线1)12()1(llO（-2,1）BA-32O（-2,1）BA-32OBA-32平移前后两直线具有怎样位置关系平行k相等，b不相等练习：问题：的表达式；并回答以下求出直线是原点；两点，、轴于轴、直线分别交的图象如图所示，：已知直线lyxkbkxylOBA)0(所对应的函数表达式。求直线轴对称，关于与若直线22)2(lyllOBA-32OBA-32（-2,0）OBA-32练习：问题：的表达式；并回答以下求出直线是原点；两点，、轴于轴、直线分别交的图象如图所示，：已知直线lyxkbkxylOBA)0(O-32BA表达式。一条直线所对应的函数请你求出其中若能；可以画出几条？？分成面积相等的两部分把△的顶点能不能画出直线过△AOBAOB)3(练习：问题：的表达式；并回答以下求出直线是原点；两点，、轴于轴、直线分别交的图象如图所示，：已知直线lyxkbkxylOBA)0(DCO-32BA____DC90OOCOC)1(C)4(ttxylm上，则落在直线恰好的对应点，点针旋转顺时绕点，将线段连结上，在直线，如图，点练习：问题：的表达式；并回答以下求出直线是原点；两点，、轴于轴、直线分别交的图象如图所示，：已知直线lyxkbkxylOBA)0(O-32BA所对应的函数表达式。求直线对称，关于与若直线33)5(lxyll例3：某地出租车计费方法如图，x（km）表示行驶里程，y（元）表示车费，请根据图象解答下列问题：（1）该地出租车的起步价是______元；（2）求y与x之间的函数关系式；（3）若某乘客有一次乘出租车的里程为18km，则这位乘客需付出租车车费多少元？1.用待定系数法求一次函数关系式；2.用待定系数法求一次函数关系式的一般步骤：一设、二代、三解、四写3.从各种问题情景中寻找条件，确定一次函数的表达式。满足条件的两定点（x1，y1）与（x2，y2）函数解析式y=kx+b一次函数的图象直线l选取解出画出选取从数到形从形到数体现了“数形结合”的数学思想“形”“点”“方程”“表达式”