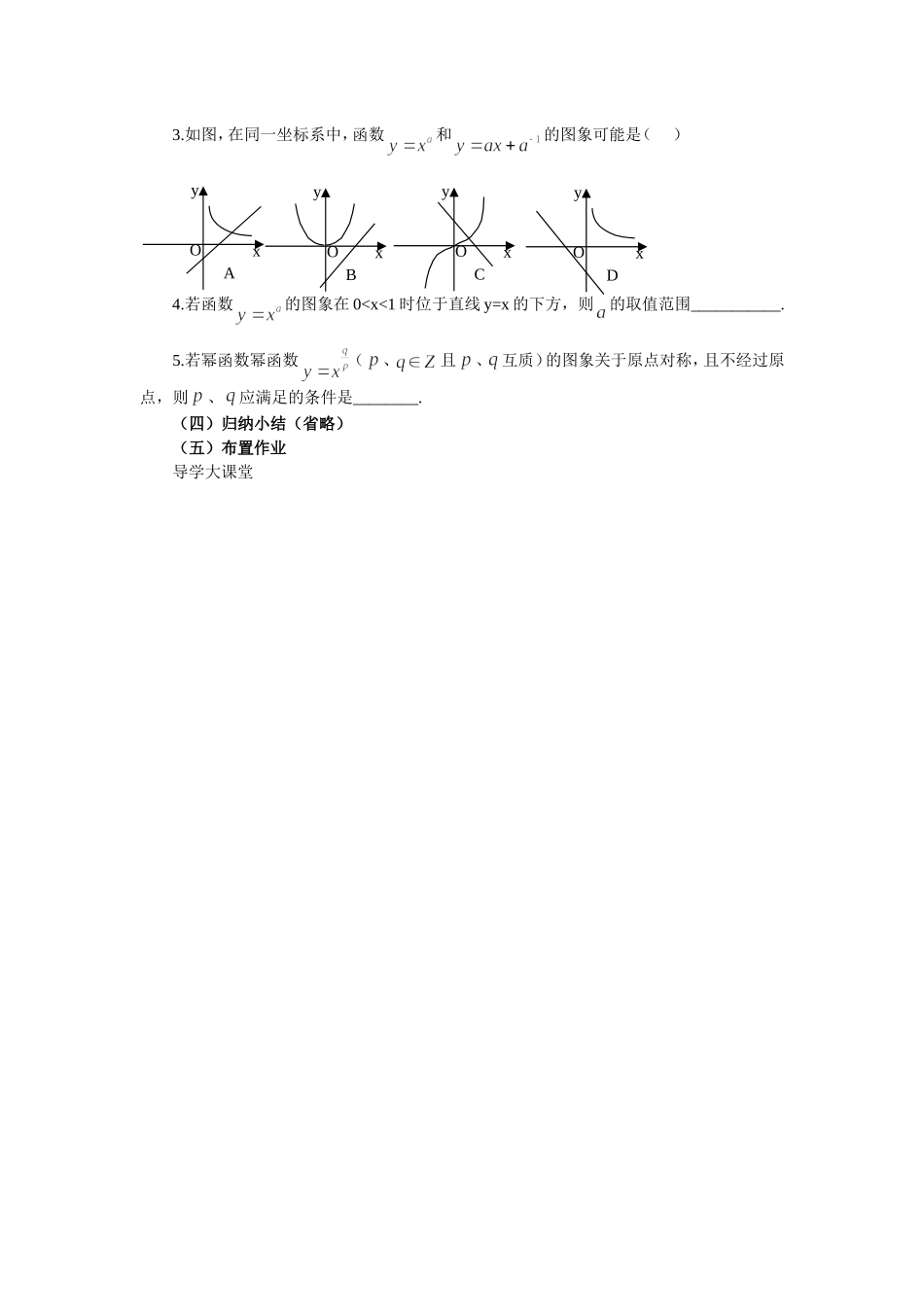
第29课幂函数(2)一.教学目标:1.知识技能(1)进一步了解幂函数的概念;(2)能综合运用幂函数的图象和性质解题。2.过程与方法通过典型问题的研究与探索,进一步掌握幂函数的图象和性质.3.情感、态度、价值观(1)进一步渗透数形结合与类比的思想方法;(2)通过综合问题的研究,提高思维品质。二.重点、难点重点:幂函数的概念、图象和性质。难点:幂函数图象与性质的综合应用。三.学法与教具(1)学法:通过类比、思考、交流、讨论,学会运用幂函数的概念和性质解题。(2)教学用具:多媒体四.教学过程:(一)复习回顾1.什么是幂函数?它有哪些共同性质?2.作幂函数图象的一般步骤是什么?3.完成下列练习:⑴下列函数中既是单调增函数,又是奇函数的是()(A)(B)(C)(D)⑵幂函数的图象过点,则的取值应是()(A)3或(B)(C)3(D)⑶当时,幂函数的图象恒在的下方,则的取值范围是()(A)(B)(C)(D)(二)例题选讲例1.已知点在幂函数的图象上,点在幂函数的图象上,则当为何值时:⑴;⑵;⑶?练习:已知,试求的取值范围。例2.指出函数的单调区间,并比较的大小.解:原函数可化为,则的图象可以由幂函数图象向左平移2个单位,再沿轴向上平移一个单位得到,所以的图象关于直线对称,且在递增,在上递减.由对称性可知:,而,所以。例3.已知幂函数的图象与轴、轴都无交点,且关于轴对称,试确定的解析式,并画出它的图象.解:由题意得,又,。但是偶函数,则是偶数,得。当和时,解析式为;当时解析式为.(图略)例4.已知,求实数的取值范围。解:由函数在上是增函数,得,。变式1:已知,求实数的取值范围。解:结合函数的图象可得:,。变式2:已知,求实数的取值范围。解:结合函数的图象可得:①;或②;或③(三)巩固练习1.函数的奇偶性是()A.奇函数B.偶函数C.非奇非偶函数D.奇偶性与有关2.幂函数的图象如图,则的值可能是()A.0B.1C.2D.311xyO3.如图,在同一坐标系中,函数和的图象可能是()4.若函数的图象在0