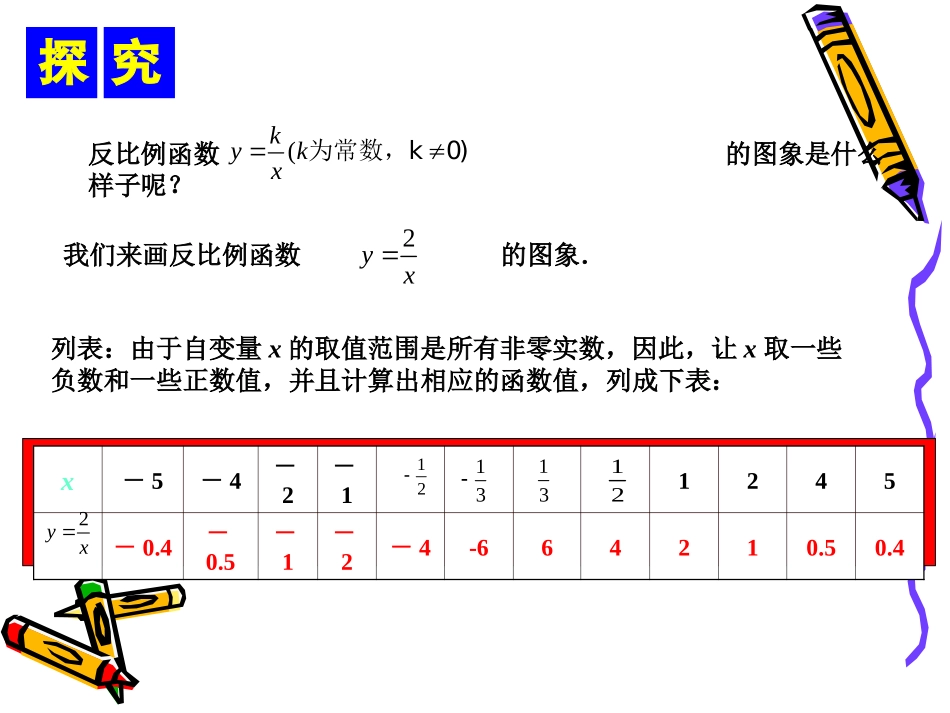
1.什么是函数的图象?建立平面直角坐标系,以自变量取的每一个值为横坐标,相应的函数值为纵坐标,描出对应的点,由所有这些点组成的图形称为这个函数的图象一次函数的图象是一条直线2.一次函数的图象是什么样子?(0)ykxbk反比例函数的图象是什么样子呢?(kykx为常数,k0)2yxx-5-4-2-11245-0.4-0.5-1-2-4-664210.50.4121313122yx列表:由于自变量x的取值范围是所有非零实数,因此,让x取一些负数和一些正数值,并且计算出相应的函数值,列成下表:我们来画反比例函数的图象.246246-2-4-6-2-4-6x-5-4-2-11245-0.4-0.5-1-2-4-664210.50.4121313122yx描点:在平面直角坐标系内,以x取的值为横坐标,相应的函数值为纵坐标,描出相应的点.如图.连线:我们可以把y轴右边的各点左边的各点,分别用一条光滑的曲线连起来.(左边也如此)列表246246-2-4-6-2-4-6观察和分析y轴右边的点,当横坐标x逐渐增大时,纵坐标y反而减小y轴左边的点也有这一性质自变量x的变化与函数y值的关系?当k>0时,反比例函数的图象也有上述性质,于是我们以后在画反比例函数的图象时,就只要“列表、描点、连线”三个步骤就可以了,不用每次都写“观察分析”kyx(0)kykx画下列反比例函数的图象4(1)yx1(2)2yx列表x-4-3-2-11234-1-2-4-884214yx12124343描点连线246246-2-4-6-2-4-64(1)yx列表x-3-2-1123-1112yx1212161614121214246246-2-4-6-2-4-61(2)2yx描点连线课堂小结•通过本节课的学习,你对反比例函数的图象和性质有了解了吗?•你还存在哪些疑问?课后作业•完成课本课后:习题