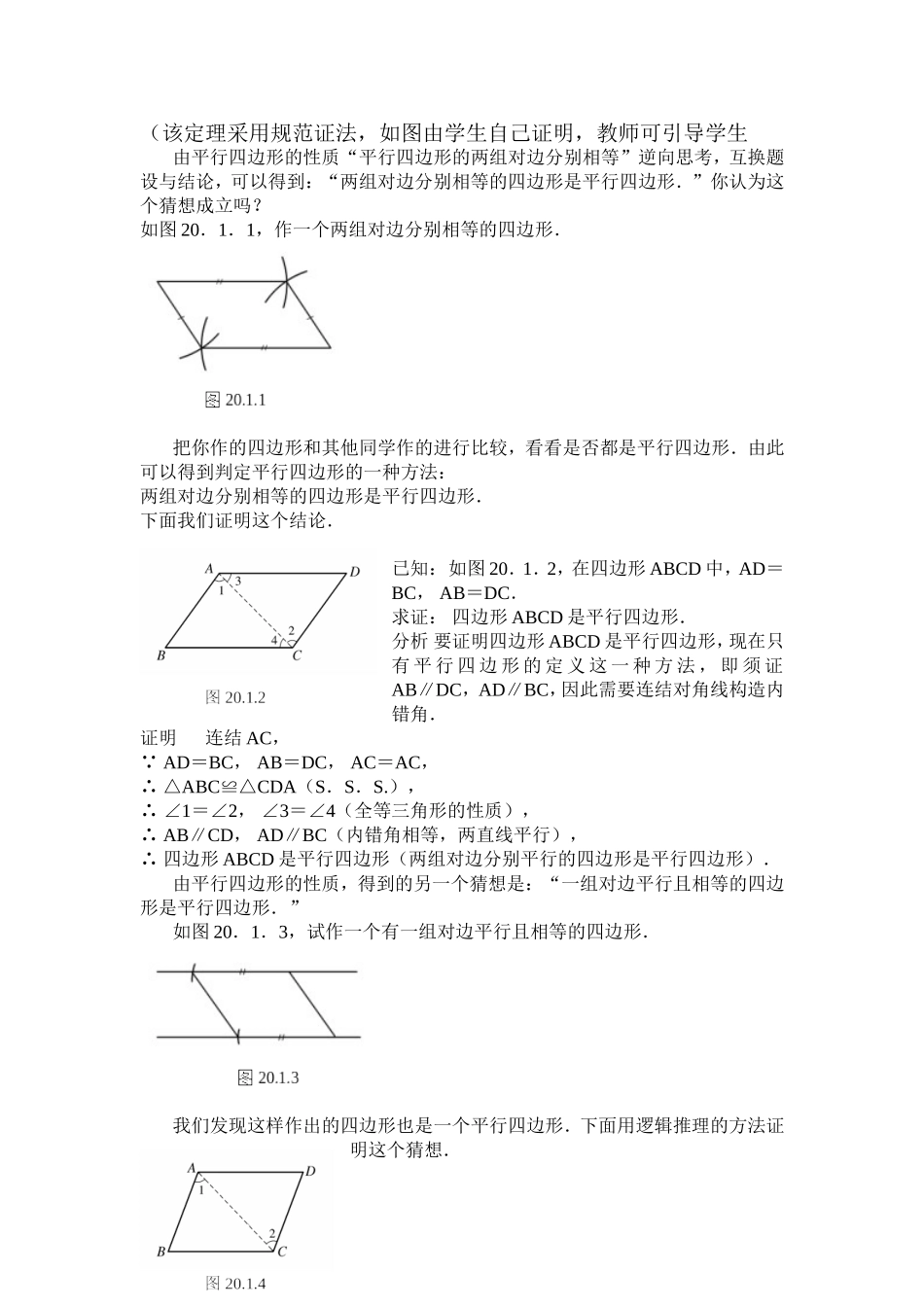
平行四边形的判定一知识教学点1.掌握平行四边形的判定定理1、2,并能与性质定理、定义综合应用。2.使学生理解判定定理与性质定理的区别与联系。3.会根据简单的条件画出平行四边形,并说明画图的依据是哪几个定理。(二)能力训练点1.通过“探索式试明法”开拓学生思路,发展学生思维能力。2.通过教学,使学生逐步学会分别从题设或结论出发寻求论证思路的分析方法,进一步提高学生分析问题,解决问题的能力。(三)德育渗透点通过一题多解激发学生的学习兴趣。(四)美育渗透点通过学习,体会几何证明的方法美。二、学法引导构造逆命题,分析探索证明,启发讲解。三、重点·难点·疑点及解决办法1.教学重点:平行四边形的判定定理1、2、的应用。2.教学难点:综合应用判定定理和性质定理。3.疑点及解决办法:在综合应用判定定理及性质定理时,在什么条件下用判定定理,在什么条件下用性质定理(强调在求证平行四边形时用判定定理,在已知平行四边形时用性质定理)。四、课时安排(2课时)五、教具学具准备投影仪,投影胶片,常用画图工具,课件六、师生互动活动设计复习引入,构造逆命题,画图分析,讨论证法,巩固应用。七、教学步骤【复习提问】1.平行四边形有什么性质?2将以上性质定理分别用命题的形式叙述出来。【引入新课】用投影仪打出上述命题的逆命题。上述第一个逆命题显然是正确的,因为它就是平行四边形的定义,所以它也是我们判定一个四边形是否为平行四边形的基本方法(定义法)。那么其它逆命题是否正确呢?如果正确就可得到另外的判定方法(写出命题)。【讲解新课】1.平行四边形的判定我们知道,平行四边形的两组对边分别相等,反过来两组对边分别相等相等的四边形是平行四边形吗?边平行且且相等的四边形是平行四边形。(该定理采用规范证法,如图由学生自己证明,教师可引导学生由平行四边形的性质“平行四边形的两组对边分别相等”逆向思考,互换题设与结论,可以得到:“两组对边分别相等的四边形是平行四边形.”你认为这个猜想成立吗?如图20.1.1,作一个两组对边分别相等的四边形.把你作的四边形和其他同学作的进行比较,看看是否都是平行四边形.由此可以得到判定平行四边形的一种方法:两组对边分别相等的四边形是平行四边形.下面我们证明这个结论.已知:如图20.1.2,在四边形ABCD中,AD=BC,AB=DC.求证:四边形ABCD是平行四边形.分析要证明四边形ABCD是平行四边形,现在只有平行四边形的定义这一种方法,即须证AB∥DC,AD∥BC,因此需要连结对角线构造内错角.证明连结AC, AD=BC,AB=DC,AC=AC,∴△ABC≌△CDA(S.S.S.),∴∠1=∠2,∠3=∠4(全等三角形的性质),∴AB∥CD,AD∥BC(内错角相等,两直线平行),∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).由平行四边形的性质,得到的另一个猜想是:“一组对边平行且相等的四边形是平行四边形.”如图20.1.3,试作一个有一组对边平行且相等的四边形.我们发现这样作出的四边形也是一个平行四边形.下面用逻辑推理的方法证明这个猜想.已知:如图20.1.4,在四边形ABCD中,AB∥CD且AB=CD.求证:四边形ABCD是平行四边形.分析要证明四边形ABCD是平行四边形,可以用平行四边形的定义,也可以用前面得到的平行四边形的判定方法.证明连结对角线AC, AB∥CD,∴∠1=∠2(两直线平行,内错角相等).又 AB=CD,AC=AC,∴△ABC≌△CDA(S.A.S.),∴BC=AD(全等三角形的性质),∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).由此我们得到平行四边形的另一种判定方法:一组对边平行且相等的四边形是平行四边形.“平行且相等”常用符号“”来表示.如图20.1.4,AB=CD且AB∥CD,可以记作“ABCD”,读作“AB平行且等于CD”.例1如图20.1.5,在ABCD中,E、F分别是对边BC和AD上的两点,且AF=CE,求证:四边形AECF为平行四边形.分析我们已经有了三种判定平行四边形的方法,根据已知条件有AF=CE,若运用现在得到的判定方法,只须证明AF∥CE.证明 四边形ABCD是平行四边形,∴AD∥BC(平行四边形的对边平行),即AF...