二次函数图象及性质习题课赵克勤VIP免费

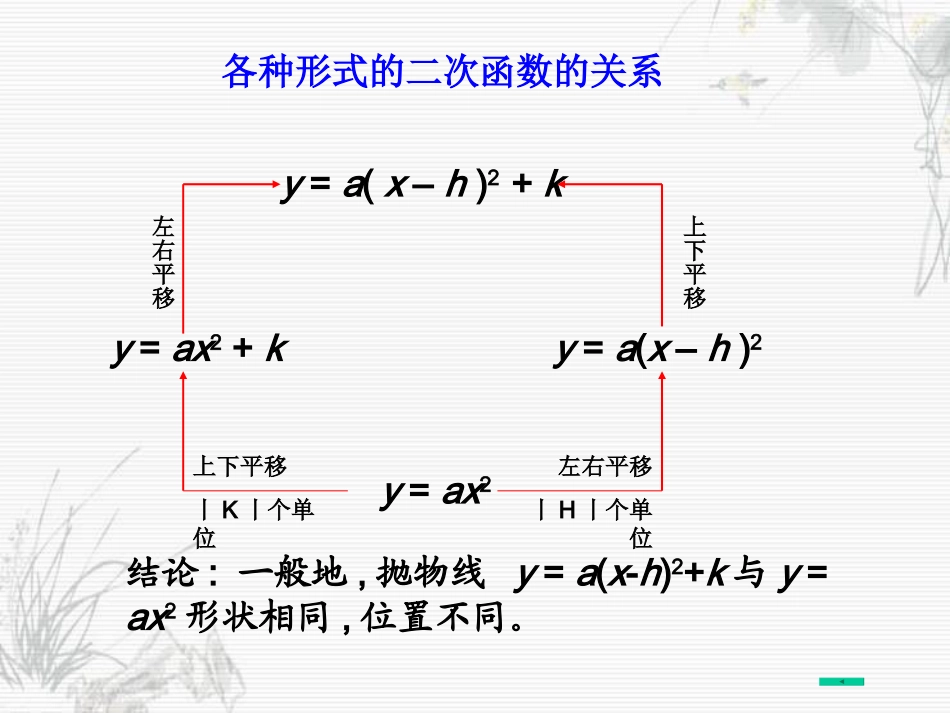
甘溪初级中学赵克勤二次函数图象及性质习题课抛物线开口方向顶点坐标对称轴最值a>0a<0增减性a>0a<02axycaxy22)(hxaykhxay2)(cbxaxy2二次函数的图象及性质当a>0时开口向上，当a<0时开口向下(0,0)(0,c)(h,0)(h,k))44,2(2abacababx2直线y轴直线hx直线hx在对称轴左侧，y随x的增大而减小在对称轴右侧，y随x的增大而增大在对称轴左侧，y随x的增大而增大在对称轴右侧，y随x的增大而减小xyxy00最小时，yx00最大时yxcyx最小时，0cyx最大时00最小时yhx0最大时yhxkyhx最小时kyhx最大时abacyabx4242最小时，abacyabx4242最大时，y轴y=ax2y=ax2+ky=a(x–h)2y=a(x–h)2+k上下平移丨K丨个单位左右平移丨H丨个单位上下平移左右平移结论:一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同。各种形式的二次函数的关系D1.关于二次函数，下列说法错误的是（）A.开口向下B.顶点坐标是(0,0)C.对称轴是y轴D.当x=0时，y有最小值为02.对于抛物线与抛物线，下列说法正确的是（）A.对称轴不同B.顶点坐标相同C.都有最高点D.不能互相平移得到C2xy232xy1322xy3.二次函数的图象向左平移3个单位，得到新的函数解析式为（）A.B.C.D.4.抛物线的对称轴是（）A.B.C.D.2xy32xy32xy2)3(xy2)3(xyC12532xxy65x直线65x直线35x直线35x直线A5.抛物线先向下平移2个单位，再向右平移1个单位，所得抛物线的解析式为＿＿＿＿＿变式一：将抛物线先向右平移２个单位，再向上平移４个单位，所得抛物线的顶点坐标是＿＿＿＿23xy2)1(32xy2)1(2xy（３,4）变式二：若抛物线先向右平移1个单位，再向上平移5个单位二次函数得抛物线为y=-3(x-1)２＋5，那么原函数解析式为。y=-3x２６.已知二次函数，回答下列问题：(1)确定抛物线的开口方向、对称轴和顶点；(2)画出此函数的大致图象；(3)说出此抛物线是由抛物线怎样平移得到的？(4)结合图象谈一谈，此函数还有哪些性质？32-2xxy2-xy通过这节课的学习，你有什么收获？