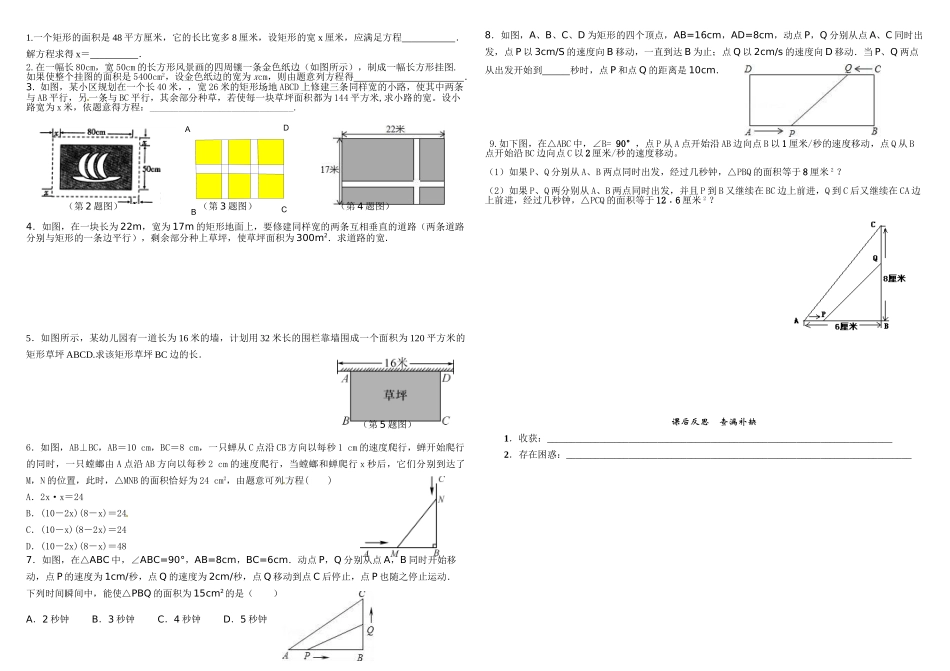
智力大挑战2.6应用一元二次方程第1课时利用一元二次方程求解几何问题【学习目标】学会利用一元二次方程的知识解决实际问题,将实际问题转化为数学模型。INCLUDEPICTURE"C:\\DocumentsandSettings\\Administrator\\桌面\\教案·北师9数(上)\\旧知回顾.TIF"\*MERGEFORMATINET1.解一元二次方程的基本方法有:(1);(2);(3);(4).2.一元二次方程解法的选择顺序一般为:→→,若没有特殊说明一般不选用.3.列一元二次方程解应用题的一般步骤:自学互研生成能力INCLUDEPICTURE"C:\\DocumentsandSettings\\Administrator\\桌面\\教案·北师9数(上)\\自主探究.TIF"\*MERGEFORMATINET探究一:如图,在长方形钢片上挖去一个长方形,制成一个四周宽相等的长方形框.已知长方形钢片的长为30cm,宽为20cm,要使挖去的长方形的面积为200cm2,求这个长方形框的框边宽.INCLUDEPICTURE"C:\\DocumentsandSettings\\Administrator\\桌面\\教案·北师9数(上)\\合作探究.TIF"\*MERGEFORMATINET典例讲解:例1:如图,在一块长35m、宽26m的矩形地面上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,要使剩余部分的面积为850m2,道路的宽应为多少?变式练习:探究二:有关“动点”的运动问题(1)关键——以静代动把动的点进行转换,变为线段的长度,(2)方法——时间变路程求“动点的运动时间”可以转化为求“动点的运动路程”,也是求线段的长度;(3)常找的数量关系——面积、勾股定理等由此,学会把动点的问题转化为静点的问题,是解这类问题的关键。例2:如图,在△ABC中,∠B=90°,BC=8cm,AB=6cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,其中一点到终点,另一点也随之停止,则几秒后△PBQ的面积等于8cm2?练习2:如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时由A、B两点出发,分别沿AC、BC方向向点C以1cm/s的速度匀速移动(到点C为止),经过几秒后Rt△PCQ的面积为Rt△ACB面积的一半?DCBA1.一个矩形的面积是48平方厘米,它的长比宽多8厘米,设矩形的宽x厘米,应满足方程.解方程求得x=.2.在一幅长80cm,宽50cm的长方形风景画的四周镶一条金色纸边(如图所示),制成一幅长方形挂图.如果使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,则由题意列方程得.3.如图,某小区规划在一个长40米,,宽26米的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AB平行,另一条与BC平行,其余部分种草,若使每一块草坪面积都为144平方米,求小路的宽。设小路宽为x米,依题意得方程:______________________________.(第2题图)(第3题图)(第4题图)4.如图,在一块长为22m,宽为17m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300m2.求道路的宽.5.如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长.(第5题图)6.如图,AB⊥BC,AB=10cm,BC=8cm,一只蝉从C点沿CB方向以每秒1cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24cm2,由题意可列方程()A.2x·x=24B.(10-2x)(8-x)=24C.(10-x)(8-2x)=24D.(10-2x)(8-x)=487.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间瞬间中,能使△PBQ的面积为15cm2的是()A.2秒钟B.3秒钟C.4秒钟D.5秒钟8.如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A、C同时出发,点P以3cm/S的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P、Q两点从出发开始到秒时,点P和点Q的距离是10cm.9.如下图,在△ABC中,∠B=90°,点P从A点开始沿AB边向点B以1厘米/秒的速度移动,点Q从B...