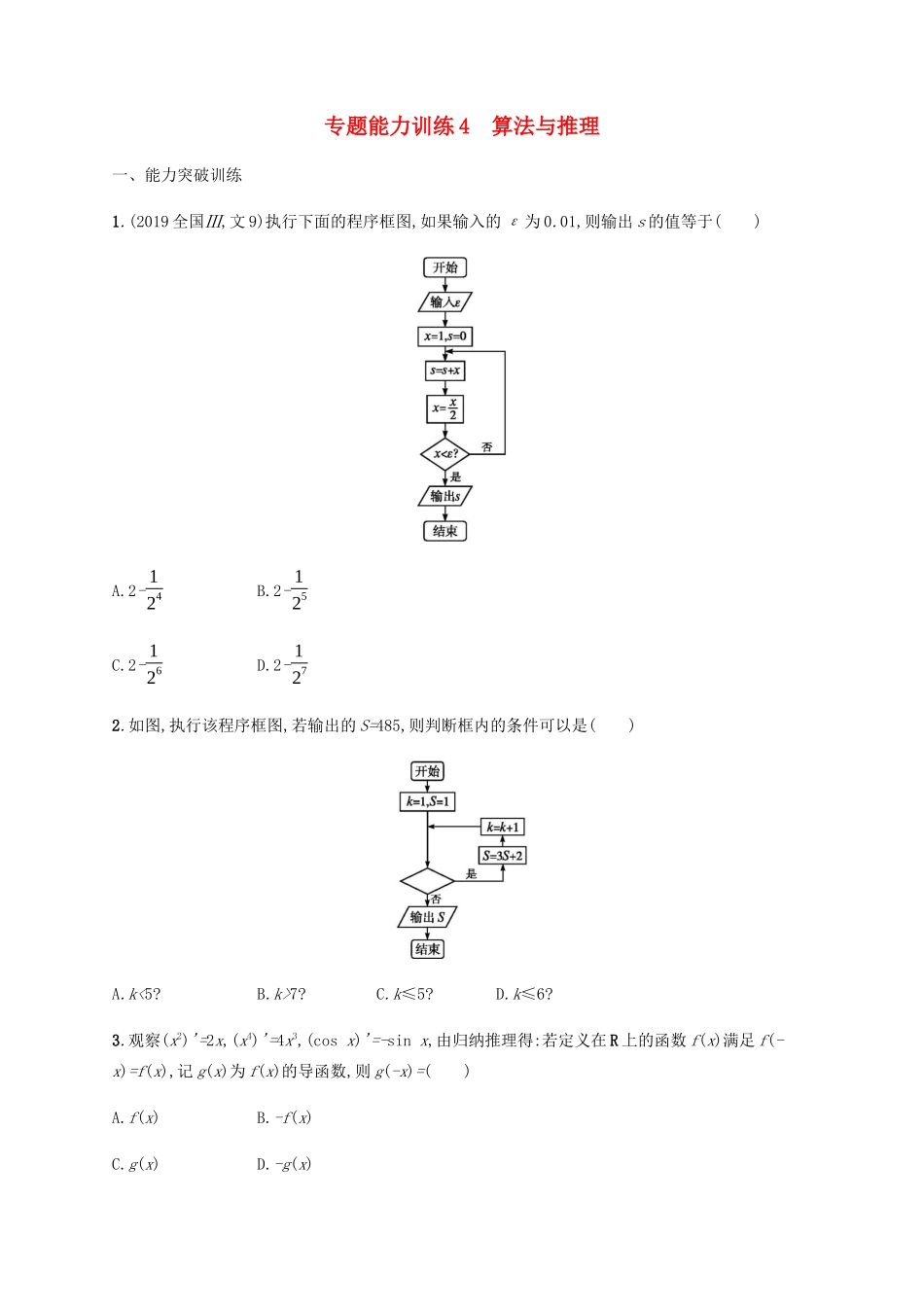
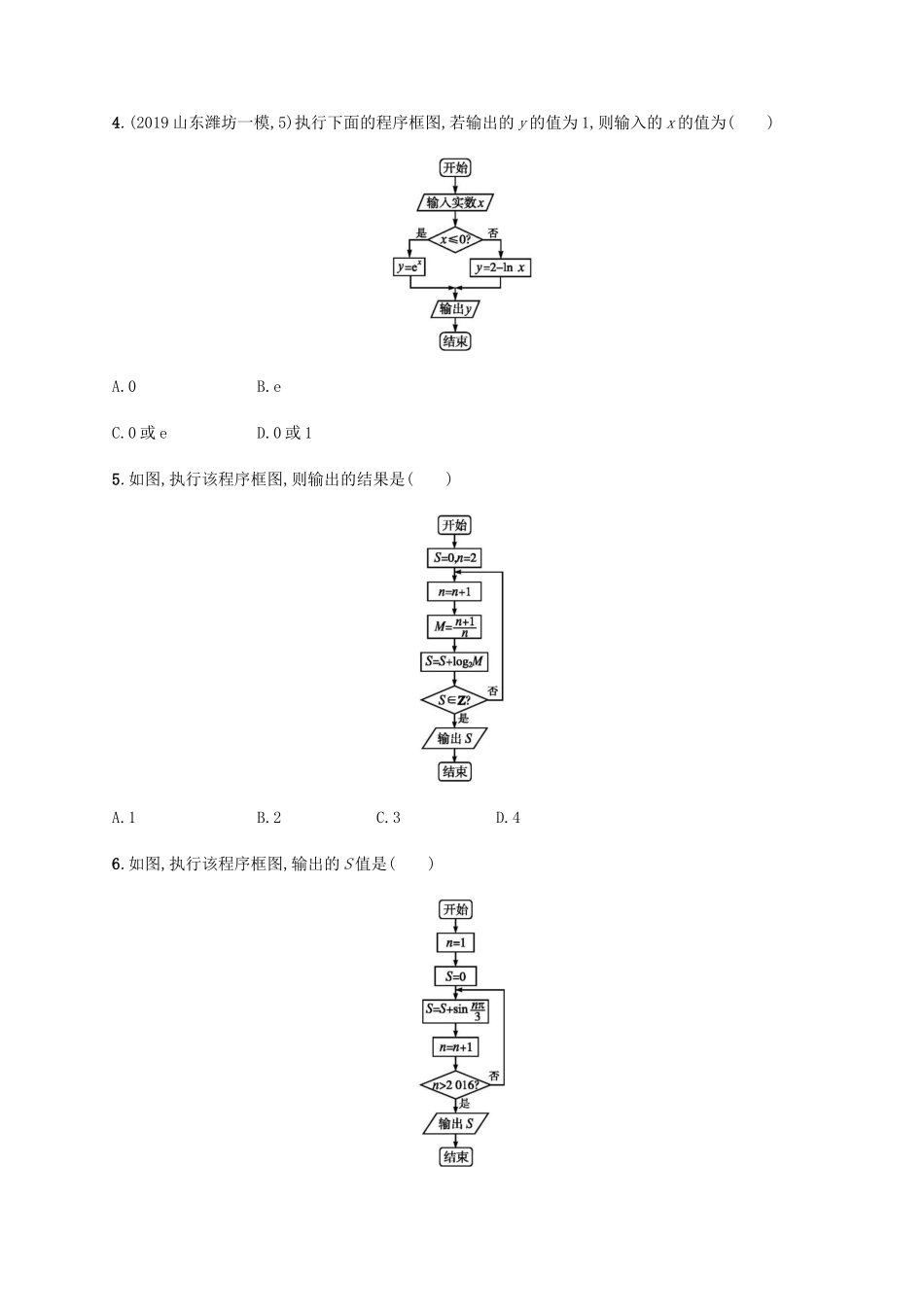
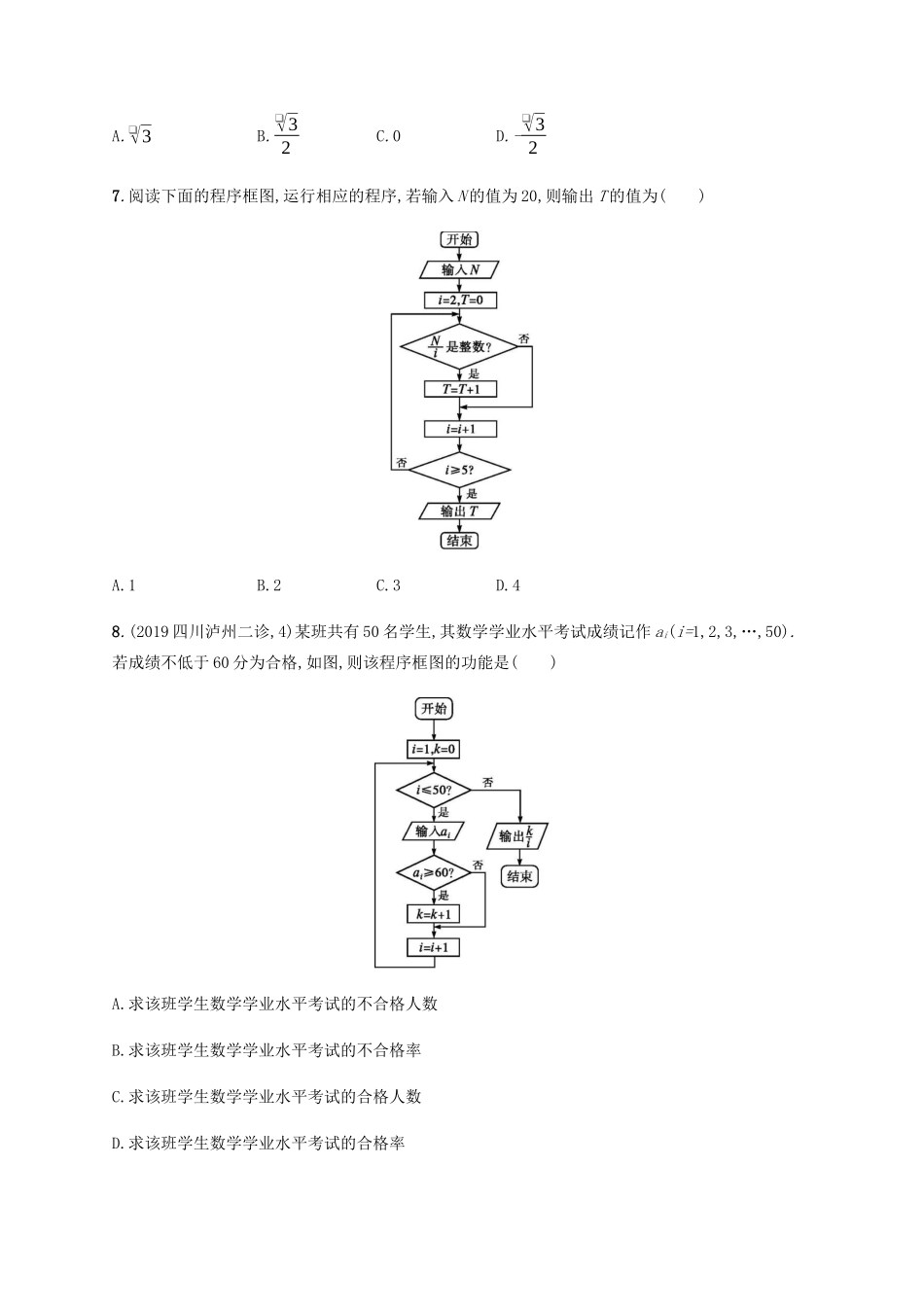
专题能力训练4算法与推理一、能力突破训练1.(2019全国Ⅲ,文9)执行下面的程序框图,如果输入的ε为0.01,则输出s的值等于()A.2-124B.2-125C.2-126D.2-1272.如图,执行该程序框图,若输出的S=485,则判断框内的条件可以是()A.k<5?B.k>7?C.k≤5?D.k≤6?3.观察(x2)'=2x,(x4)'=4x3,(cosx)'=-sinx,由归纳推理得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)=()A.f(x)B.-f(x)C.g(x)D.-g(x)4.(2019山东潍坊一模,5)执行下面的程序框图,若输出的y的值为1,则输入的x的值为()A.0B.eC.0或eD.0或15.如图,执行该程序框图,则输出的结果是()A.1B.2C.3D.46.如图,执行该程序框图,输出的S值是()A.❑√3B.❑√32C.0D.-❑√327.阅读下面的程序框图,运行相应的程序,若输入N的值为20,则输出T的值为()A.1B.2C.3D.48.(2019四川泸州二诊,4)某班共有50名学生,其数学学业水平考试成绩记作ai(i=1,2,3,…,50).若成绩不低于60分为合格,如图,则该程序框图的功能是()A.求该班学生数学学业水平考试的不合格人数B.求该班学生数学学业水平考试的不合格率C.求该班学生数学学业水平考试的合格人数D.求该班学生数学学业水平考试的合格率9.观察等式:f(13)+f(23)=1;f(14)+f(24)+f(34)=32;f(15)+f(25)+f(35)+f(45)=2;f(16)+f(26)+f(36)+f(46)+f(56)=52;……由以上几个等式的规律可猜想f(12019)+f(22019)+f(32019)+…+f(20172019)+f(20182019)=.10.执行下面的程序框图,若输入n的值为3,则输出的S的值为.11.(2019黑龙江高考模拟,14)已知命题:在平面直角坐标系xOy中,椭圆x2a2+y2b2=1(a>b>0),△ABC的顶点B在椭圆上,顶点A,C分别为椭圆的左、右焦点,椭圆的离心率为e,则sinA+sinCsinB=1e.现将该命题类比到双曲线中,△ABC的顶点B在双曲线上,顶点A,C分别为双曲线的左、右焦点,设双曲线的方程为x2a2−y2b2=1(a>0,b>0),双曲线的离心率为e,则有.12.某学习小组由学生和教师组成,人员构成同时满足以下三个条件:①男学生人数多于女学生人数;②女学生人数多于教师人数;③教师人数的两倍多于男学生人数.(1)若教师人数为4,则女学生人数的最大值为;(2)该小组人数的最小值为.二、思维提升训练13.(2019湖南益阳二模,10)我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:“今有蒲生一日,长三尺,莞生一日,长一尺.蒲生日自半,莞生日自倍.问几何日而长等?”(蒲常指一种多年生草本植物,莞指水葱一类的植物)现欲知几日后,莞高超过蒲高一倍.为了解决这个新问题,设计的程序框图如图所示,输入A=3,a=1,则在①处应填的内容和输出i的值分别为()A.S>2T?,4B.S<2T?,4C.T>2S?,3D.T<2S?,314.如图,执行该程序框图,输出的S为()A.3B.43C.12D.-215.如图,执行该程序框图,若f(x)在区间[-1,a]上的值域为[0,2],则实数a的取值范围是()A.(0,1]B.[1,❑√3]C.[1,2]D.[❑√3,2]16.箱子里有16张扑克牌:红桃A,Q,4,黑桃J,8,7,4,3,2,草花K,Q,6,5,4,方块A,5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话.学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是()A.草花5B.红桃QC.红桃4D.方块517.如下是按一定规律排列的三角形等式表,现将等式从左至右,从上到下依次编上序号,即第一个等式为20+21=3,第二个等式为20+22=5,第三个等式为21+22=6,第四个等式为20+23=9,第五个等式为21+23=10,……,依此类推,则第99个等式为()20+21=320+22=521+22=620+23=921+23=1022+23=1220+24=1721+24=1822+24=2023+24=24……A.27+213=8320B.27+214=16512C.28+214=16640D.28+213=844818.下面程序框图的输出结果为.19.(2019四川成都高三一诊,15)公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.利用刘徽的“割圆术”思想设计的一个程序框图如图所示,则输出的n的值为.(参考数据:sin15°≈0.2588,sin7.5°≈0.1305)20....