反比例函数的图象和性质(2)-(2)VIP免费

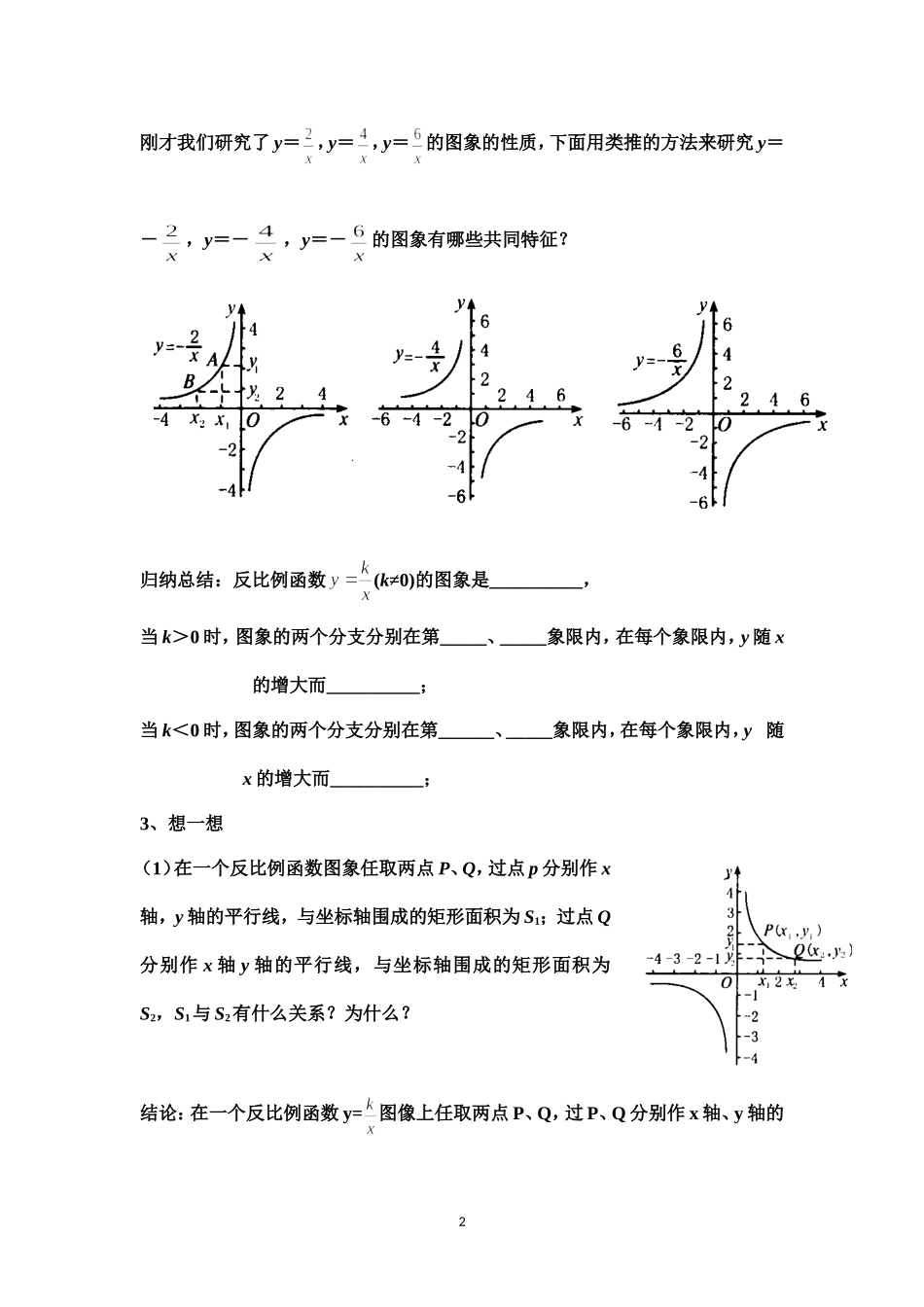
6.2.2反比例函数的图象和性质（2）学习目标:1．逐步提高从函数图象中获取信息的能力，2、探索并掌握反比例函数的主要性质．学习重点：通过观察图象，归纳概括反比例函数图象的共同特征，探索反比例函数的主要性质。学习难点：从反比例函数的图象中归纳总结反比例函数的主要性质。学法指导：类比，观察、合作探究，引导发现学习过程一、温故知新1、反比例函数的图象是什么？2、反比例函数的图象的位置与k有怎样关系？二、探索新知、1、观察反比例函数y＝，y＝，y＝的图象，你能发现它们有什么共同特征？1）图像分别位于哪几个象限？2）在每一个象限内，随着x值的增大．y的值是怎样变化的？能说明这是为什么吗？2、议一议1刚才我们研究了y＝，y＝，y＝的图象的性质，下面用类推的方法来研究y＝－，y＝－，y＝－的图象有哪些共同特征？归纳总结：反比例函数(k≠0)的图象是__________，当k＞0时，图象的两个分支分别在第_____、_____象限内，在每个象限内，y随x的增大而__________；当k＜0时，图象的两个分支分别在第______、_____象限内，在每个象限内，y随x的增大而__________；3、想一想（1）在一个反比例函数图象任取两点P、Q，过点p分别作x轴，y轴的平行线，与坐标轴围成的矩形面积为S1；过点Q分别作x轴y轴的平行线，与坐标轴围成的矩形面积为S2，S1与S2有什么关系？为什么？结论：在一个反比例函数y=图像上任取两点P、Q，过P、Q分别作x轴、y轴的2平行线，与坐标轴围成的矩形面积分别为S1、S2，则S1S2三、活学活用巩固提高1.下列函数中，其图象位于第一，三象限的有；在其图象所在象限内，y的值随x值的增大而增大的有。①y=②y=③y=④y=2.已知点(2,y1),(3,y2)在反比例函数y=的图像上，则y1y2.3.已知点(x1,y1),(x2,y2)都在反比例函数的图象上，且x1＜x2＜0,则y1y2。4.已知点A（11xy，）、B（22xy，）是反比例函数xky（0k）图象上的两点，若210xx，则()A．210yyB．120yyC．021yyD．012yy5、点，都在反比例函数的图象上，若，则的大小关系是．6.反比例函数xky的图象如图所示，点M是该函数图象上一点，MN垂直于x轴，垂足是点N，如果S△MON＝2，则k的值为.7．如图，是反比例函数的图象在第一象限分支上的一个动点，随着自变量的增大，矩形的面积（）A．不变B.增大C.减小D.无法确定3四、课时小结五、布置作业达标测试1.下列函数：①；②；③；④中（1）图象位于二、四象限的有；（2）在每一象限内，随的增大而增大的有；（3）在每一象限内，随的增大而减小的有．2.若函数的图象在其象限内，随的增大而增大，则的取值范围是．3.点，都在反比例函数的图象上，若，则的大小关系是．4、若A（x1，y1）,B(x2，y2)，C（x3，y3）都是反比例函数的图象上的点，且x1＜0＜x2＜x3，则y1，y2，y3由小到大的顺序是；5．如图，是反比例函数的图象在第一象限分支上的一个动点，过点P作连接PO，则△PAO的面积为．45