26.3实际问题与二次函数(1)VIP免费

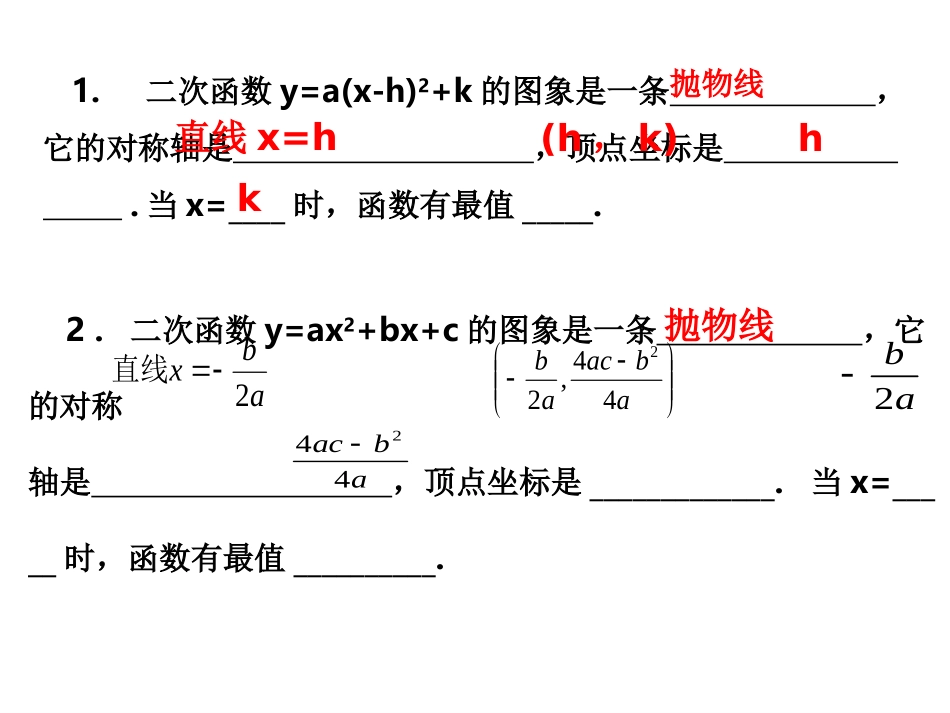
26.3实际问题与二次函数2.二次函数y=ax2+bx+c的图象是一条，它的对称轴是，顶点坐标是_____________.当x=_____时，函数有最值__________.抛物线abacab44,22abx2直线1.二次函数y=a(x-h)2+k的图象是一条，它的对称轴是，顶点坐标是.当x=____时，函数有最值_____.抛物线直线x=h(h，k)hkab2abac442某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映：如果调整价格，每涨价1元，每星期要少卖出10件；涨价多少时才能使利润达到6250元。解：设涨价多少时才能使利润达到解：设涨价多少时才能使利润达到62506250元。元。(60+x-40)(300-10x)=6250(60+x-40)(300-10x)=6250某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映：如果调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出18件，已知商品的进价为每件40元，如何定价才能使利润最大？（1）设每件涨价x元，每星期售出商品的利润为y元．则y＝(60+x-40)(300-10x)即y＝-10x2+100x+6000其中，0≤x≤30.(元)(元)(2)在降价的情况下，最大利润是多少？解：设每件降价x元，每星期售出商品的利润为y元．则某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映：如果调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出18件，已知商品的进价为每件40元，如何定价才能使利润最大？y＝(60-x-40)(300+18x)即y＝-18x2+60x+6000当60522(18)3bxa2()5518606000580033y最大值其中，0≤x≤20.∴当定价为65元时，利润最大，最大利润6250元。1.某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.如何提高售价,才能在半个月内获得最大利润?解：设销售价为x元(x≥30元),利润为y元,则20000140202xx.450035202xy=(x-20)[400-20(x-30)]解：设旅行团人数为解：设旅行团人数为xx人人,,营业额为营业额为yy元元,,则则2.2.某旅行社组团去外地旅游某旅行社组团去外地旅游,30,30人起组团人起组团,,每人单价每人单价800800元元..旅行社对超过旅行社对超过3030人的团给予优惠人的团给予优惠,,即旅行团即旅行团每增加一人每增加一人,,每人的单价就降低每人的单价就降低1010元元..你能帮助分析你能帮助分析一下一下,,当旅行团的人数是多少时当旅行团的人数是多少时,,旅行社可以获得最旅行社可以获得最大营业额？大营业额？3010800xxyxx1100102