6.2反比例函数的图象和性质VIP免费

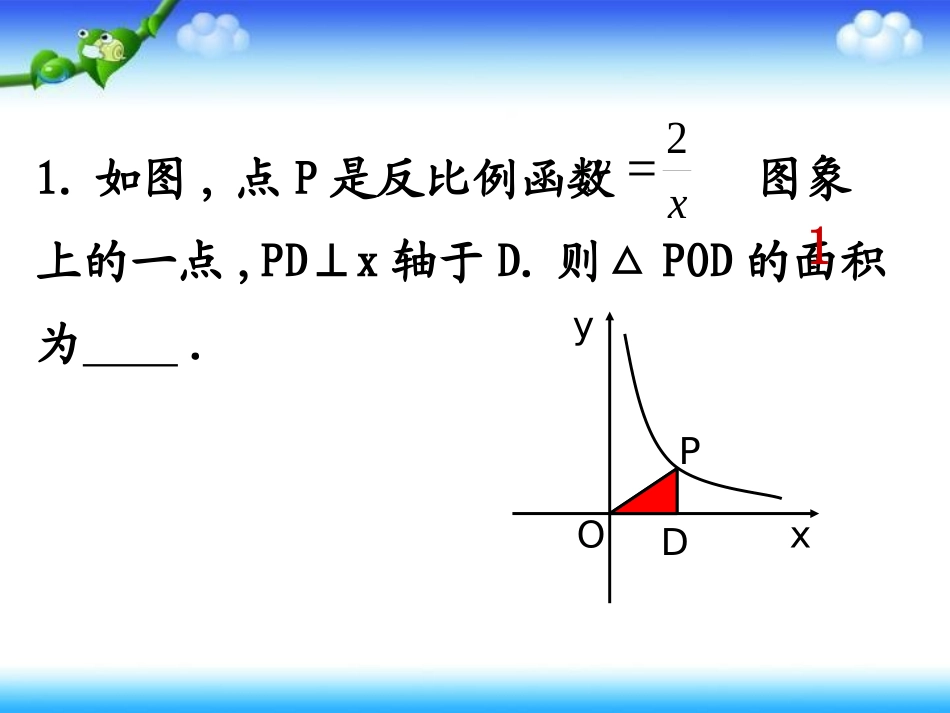
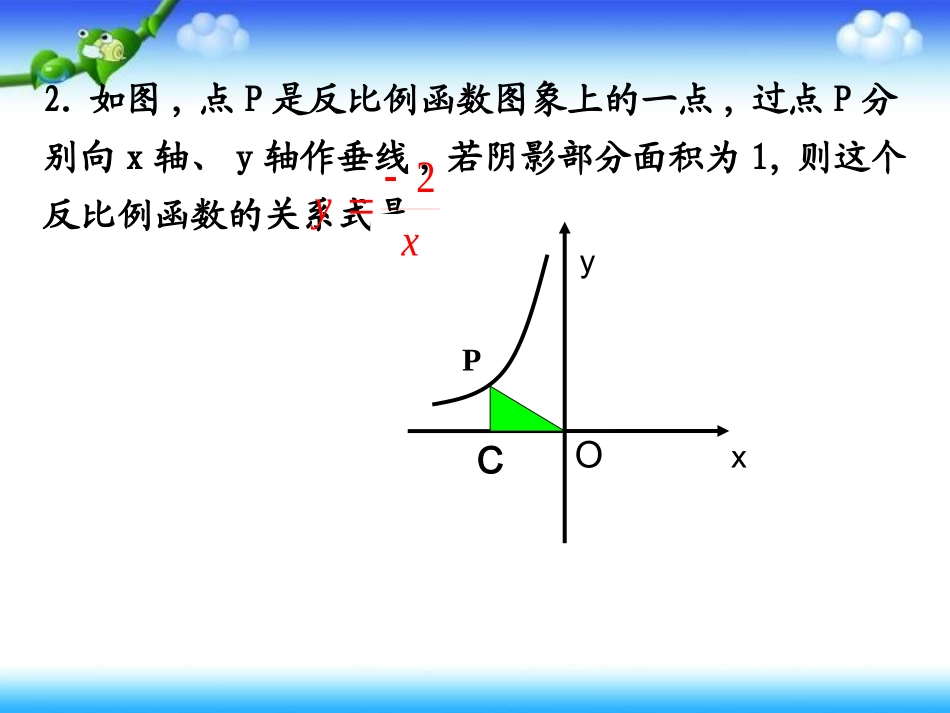
反比例函数的专题复习-----------与面积有关的问题PDOyx1.如图,点P是反比例函数图象上的一点,PD⊥x轴于D.则△POD的面积为.xy212.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为1,则这个反比例函数的关系式是.PDoyxPyxOCxy2||21||||2121knmAPOASOAPP(m,n)Aoyx则垂足为轴的垂线作过有上任意一点是双曲线设,,)1(:,)0(),(AxPkxkynmP过P作x轴的垂线，垂足为A,则它与坐标轴形成的三角形的面积为：P(m,n)AoyxB).(||||||,,,,)2(如图所示则垂足分别为轴的垂线轴分别作过矩形knmAPOASBAyxPOAPB过反比例函数图象上任一点P分别作x轴、y轴的垂线，垂足分别为A,B，它们与坐标轴形成的矩形面积为1、在双曲线上任一点分别作x轴、y轴的垂线段，与x轴y轴围成矩形面积为12，求函数解析式__________。xky(x>0)yxOxy12xy12或分类讨论思想AoyxBS1S2xy32、如图，A,B是双曲线上的点，分别经过A,B两点向x轴、y轴作垂线段，若.211SSS，则阴影4Oyxs1s2∟3、如图,点P、Q是反比例函数图象上的两点,过点P、Q分别向x轴、y轴作垂线,则S1(黄色三角形）S2(绿色三角形）的面积大小关系是：S1____S2.PQ趁热打铁，大显身手（提高篇）∟∟∟=yBAxo如图，已知，A,B是双曲线上的两点，)0(kxky（1）若A(2,3)，求K的值（2）在(1)的条件下，若点B的横坐标为3，连接OA,OB,AB，求△OAB的面积。CDEE(3,3)AEBBOCAODEDOCAOBSSSS△△△矩形△S-yBAxo如图，已知，A,B是双曲线上的两点，)0(kxky（1）若A(2,3)，求K的值（2）在(1)的条件下，若点B的横坐标为3，连接OA,OB,AB，求△OAB的面积。CDE等积变换CD=1,AC=3,BD=2ACBDAOBSS梯形△yBAxo如图，已知，A,B是双曲线上的两点，)0(kxky（1）若A(2,3)，求K的值（2）在(1)的条件下，若点B的横坐标为3，连接OA,OB,AB，求△OAB的面积。C(5,0)补成三角形5:xylAB小结与反比例函数有关的求面积问题的主要方法有•（1）根据|K|的几何意义•（2）等积变换•（3）补•（4）割AyOBxMNy=kx+1的图像交于A、B两点,点A的纵坐标是3.已知：如图,反比例函数与一次函数xy6（1）求这个一次函数的解析式（2）求△AOB的面积.变式练习一1xyN(0,1)BONAONAOBSSS△△△反比例函数面积不变性2KS———————————PQ0xy）（yx,P0xy）（yx,yoABSK一题多解—————多题同解化归，转化，分类等思想如图，已知正方形OABC的面积为9，点O为坐标原点，点A在x轴上，点C在y轴上，点B在函数y=k/x的图象上，点P(m,n)是图象上任意一点，过点P分别作x轴，y轴的垂线，垂足分别为E,F，拓展提高G若设矩形OEPF和正方形OABC不重合部分的面积为S，(1)求B点坐标和k的值；(2)当S=9/2时，求P点坐标；(3)写出S关于M的函数关系式．