正切函数图像VIP免费

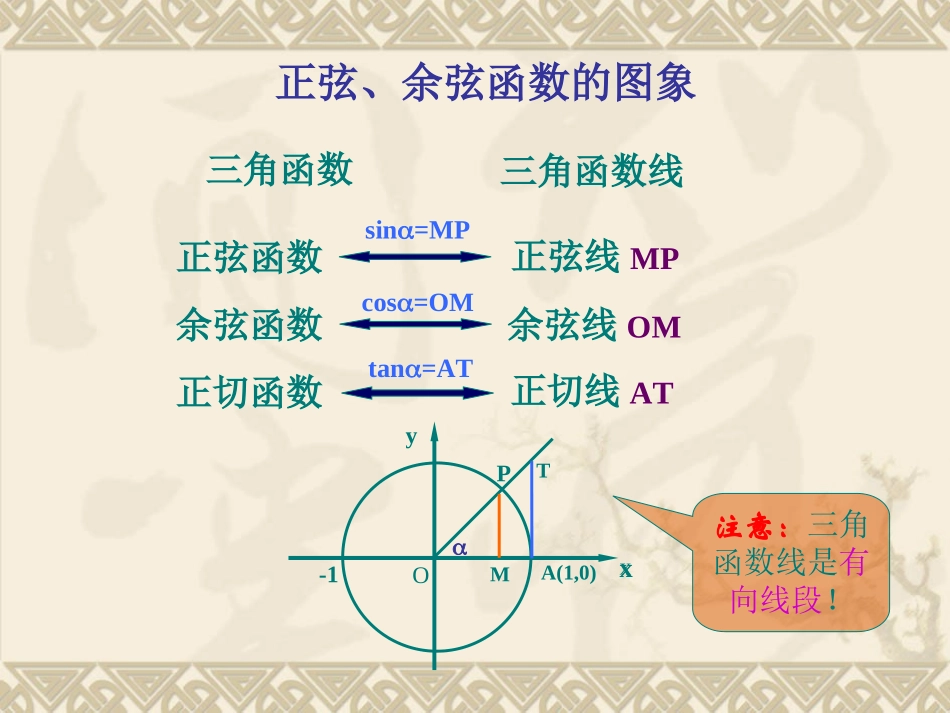
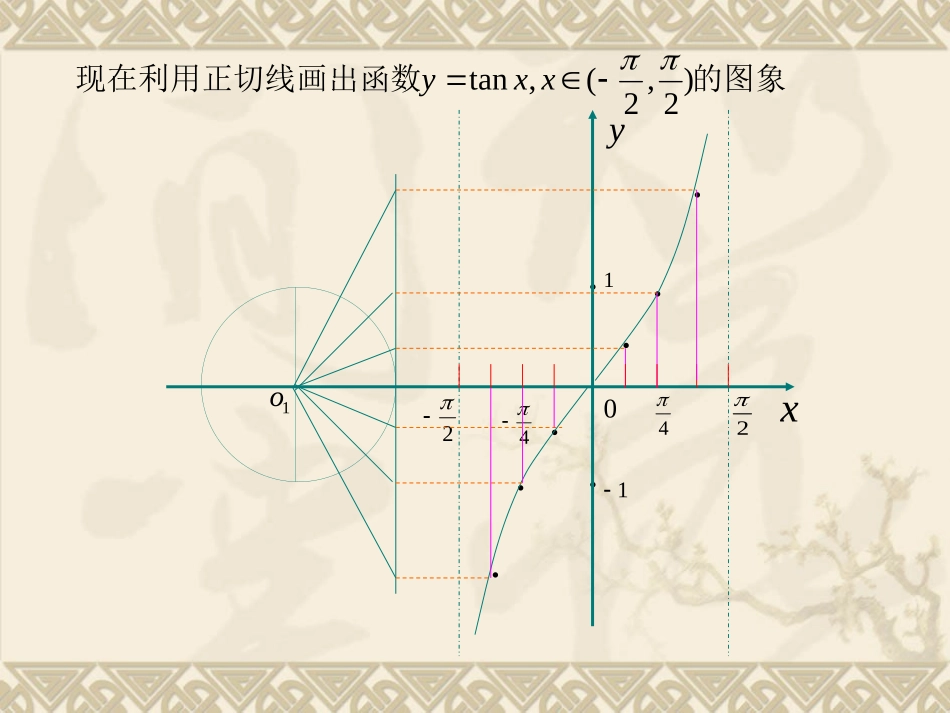
三角函数三角函数线正弦函数余弦函数正切函数正弦线MP正弦、余弦函数的图象yxxO-1PMA(1,0)Tsin=MPcos=OMtan=AT注意：三角函数线是有向线段！余弦线OM正切线AT的图象数现在利用正切线画出函)2,2(,tanxxy111oxy02442利用正切函数的周期性,把图象向左,右扩展,得到正切函数并把它的图象且,)(,2,tanZkkxRxxy叫做正切曲线.xy0223223xy0223223正切函数图象的简单画法：三点两线法。“三点”:(0,0)1144、（，）、，“两线”:22xx和xy0223223441-1结合正切函数图像研究正切函数的性质：定义域、值域、周期性、奇偶性和单调性．正切函数的性质：①定义域：Zkkxx，2②值域：R④奇偶性：O奇函数．正切曲线关于原点对称．⑤单调性:)(22Zkkkx，正切函数在每个开区间内都是增函数．⑥渐近线：Zk2kx渐近线方程是：，xy0223223xy0223223xxtantan)(2Zkkx且∴正切函数是奇函数．正切函数的主要性质如下:定义域值域周期性奇偶性单调性Zkkxx,2RT奇函数(正切曲线关于原点对称)内为增函数），，在（Zkkk22正切函数的图像和性质正切函数的图像和性质xytan（（11）的图象是利用平移正切线得到的。简单画法：三点两线法。）的图象是利用平移正切线得到的。简单画法：三点两线法。Z2kkxx，R22kk，ZkZk2kx0，kZk（2）性质:xytan定义域值域周期奇偶性单调增区间对称中心渐近线方程奇函数小结：小结：