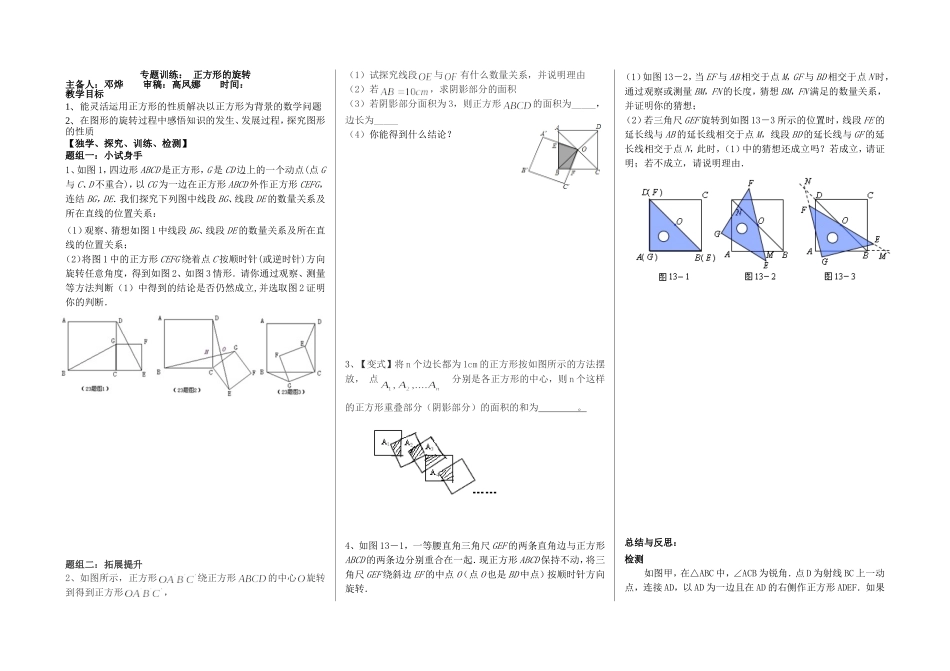
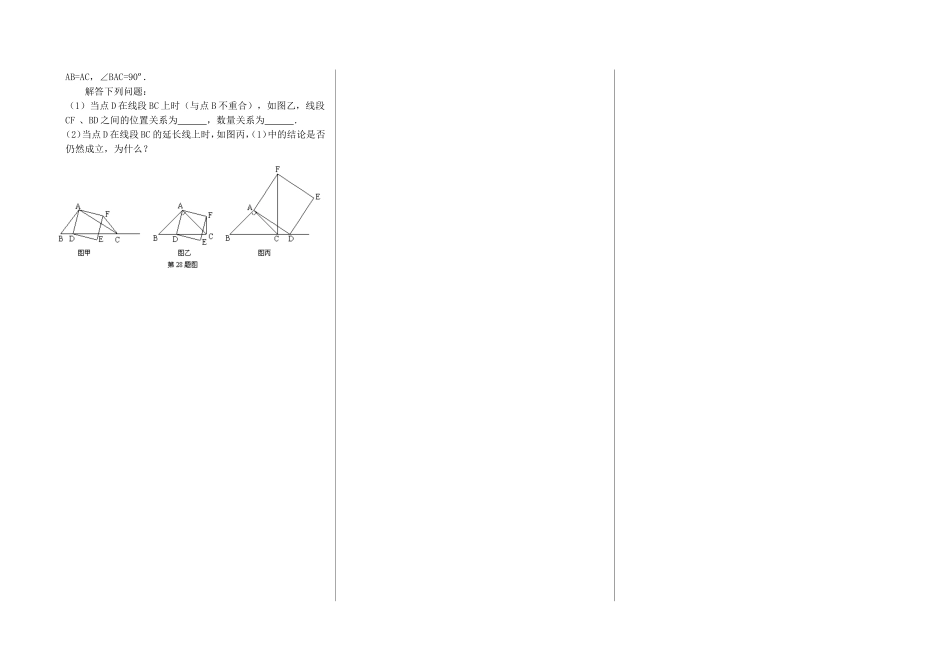
专题训练:正方形的旋转主备人:邓烨审稿:高凤娜时间:教学目标1、能灵活运用正方形的性质解决以正方形为背景的数学问题2、在图形的旋转过程中感悟知识的发生、发展过程,探究图形的性质【独学、探究、训练、检测】题组一:小试身手1、如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的数量关系及所在直线的位置关系:(1)观察、猜想如图1中线段BG、线段DE的数量关系及所在直线的位置关系;(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度,得到如图2、如图3情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图2证明你的判断.题组二:拓展提升2、如图所示,正方形绕正方形的中心旋转到得到正方形,(1)试探究线段与有什么数量关系,并说明理由(2)若,求阴影部分的面积(3)若阴影部分面积为3,则正方形的面积为_____,边长为_____(4)你能得到什么结论?3、【变式】将n个边长都为1cm的正方形按如图所示的方法摆放,点分别是各正方形的中心,则n个这样的正方形重叠部分(阴影部分)的面积的和为。4、如图13-1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.(1)如图13-2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;(2)若三角尺GEF旋转到如图13-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.总结与反思:检测如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.如果AB=AC,∠BAC=90º.解答下列问题:(1)当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为,数量关系为.(2)当点D在线段BC的延长线上时,如图丙,(1)中的结论是否仍然成立,为什么?