二次函数的图象与性质.2-二次函数的图象与性质(第2课时)演示文稿4VIP免费

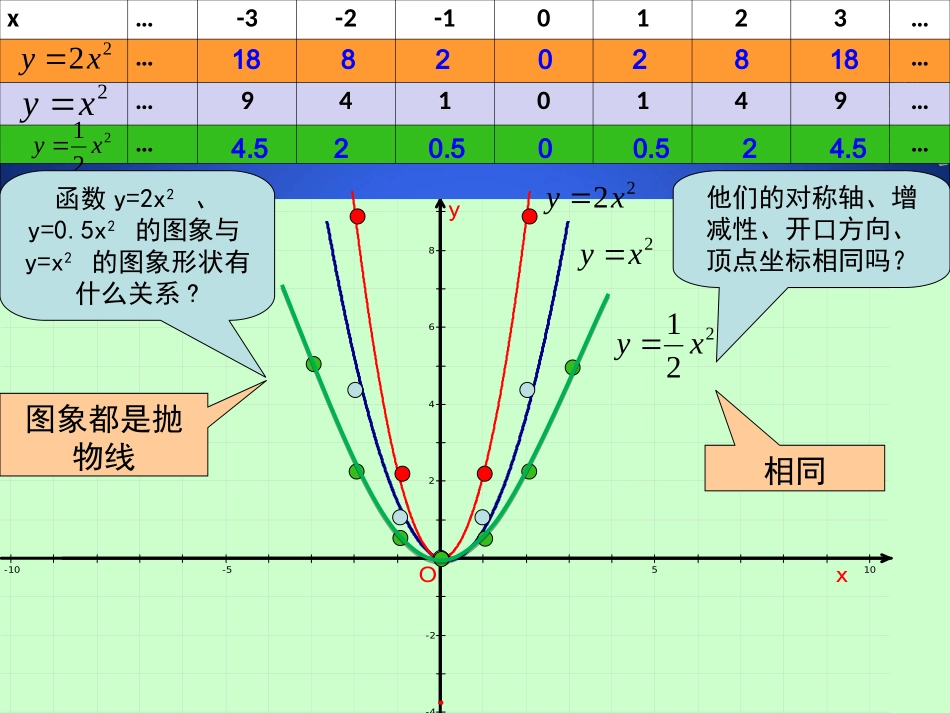
第二章二次函数2.2二次函数的图象与性质（第2课时）y=x2y=-x2图象开口方向顶点坐标对称轴增减性最值xyOyxO向上向下(0,0)(0,0)y轴(x=0)y轴(x=0)在对称轴的左侧，y随着x的增大而减小。在对称轴的右侧，y随着x的增大而增大。在对称轴的左侧,y随着x的增大而增大。在对称轴的右侧，y随着x的增大而减小。x=0时,y最小=0x=0时,y最大=08642-2-4y-10-5510xOx…-3-2-10123…………9410149………221xy2xy22xy221xy22xy2xy图象都是抛物线相同他们的对称轴、增减性、开口方向、顶点坐标相同吗？函数y=2x2、y=0.5x2的图象与y=x2的图象形状有什么关系?1882028184.520.500.524.58642-2-4y-10-5510xO8642-2-4y-10-5510xO221xy22xy2xy22xy2xy221xy当a>0时，抛物线y=ax2的开口向上，对称轴是y轴(x=0)，顶点坐标是(0,0)，在对称轴的左侧，y随x的增大而减小，在对称轴的右侧,y随x的增大而增大，当x=0时，取得最小值，这个值等于0,a越大抛物线的开口越小；当a<0时,抛物线y=ax2的开口向下，对称轴是y轴(x=0)，顶点坐标是(0,0)，在对称轴的左侧，y随x的增大而增大，在对称轴的右侧,y随x的增大而减小，当x=0时，取得最大值，这个值等于0，a越小抛物线的开口越大。y=ax2(a≠0)a>0a<0图象开口方向顶点坐标对称轴增减性最值xyOyxO向上向下(0,0)(0,0)y轴(x=0)y轴(x=0)在对称轴的左侧，y随着x的增大而减小。在对称轴的右侧，y随着x的增大而增大。在对称轴的左侧,y随着x的增大而增大。在对称轴的右侧，y随着x的增大而减小。x=0时,y最小=0x=0时,y最大=0抛物线y=ax2(a≠0)的形状是由|a|来确定的,一般说来,|a|越大,抛物线的开口就越小.(1)函数图象开口方向______,对称轴________，顶点坐标_____;函数图象开口方向______,对称轴__________，顶点坐标_______。(3)已知点（1，y1），（2，y2），（3，y3）在抛物线y=4x2的图像上，则y1,y2,y3的大小关系___________;已知点（-1,y1），（-2，y2），（-3，y3）在抛物线y=-3x2的图像上，则y1,y2,y3的大小关系__________。(2)二次函数y=ax2(a≠0)的图象经过点A（1，2），则函数y=ax2的表达式为________；若点C(-2,m),D（n,4）也在函数的图象上，则点C的坐标为______,点D的坐标为_________。232xyy10时,函数y=ax2+c的图象可由y=ax2的图象向平移个单位得到，当c<0时，函数y=ax2+c的图象可由y=ax2的图象向平移个单位得到。42-2-4-6-8y-10-5510xOy=-x2-2y=-x2+3y=-x2函数y=-x2-2的图象可由y=-x2的图象沿y轴向下平移2个单位长度得到.函数y=-x2+3的图象可由y=-x2的图象沿y轴向上平移3个单位长度得到.图象向上移还是向下移,移多少个单位长度,有什么规律吗?上加下减相同上c下|c|当a>0时，抛物线y=ax2+c的开口，对称轴是_________，顶点坐标是，在对称轴的左侧，y随x的增大而，在对称轴的右侧,y随x的增大而______，当x=时，取得最值，这个值等于；当a<0时,抛物线y=ax2+c的开口，对称轴是________，顶点坐标是，在对称轴的左侧，y随x的增大而，在对称轴的右侧,y随x的增大而，当x=时，取得最值，这个值等于。42-2-4-6-8y-10-5510xO108642-2y-10-5510xOy=-x2-2y=-x2+3y=-x2y=x2-2y=x2+1y=x2向上y轴(x=0)(0,c)减小增大0小c向下y轴(x=0)(0,c)增大减小0大c(1)函数y=4x2+5的图象可由y=4x2的图象向平移个单位得到；y=4x2-3的图象可由y=4x2的图象向平移个单位得到。(3)将抛物线y=4x2向上平移3个单位，所得的抛物线的函...