21.3二次根式的加减VIP免费

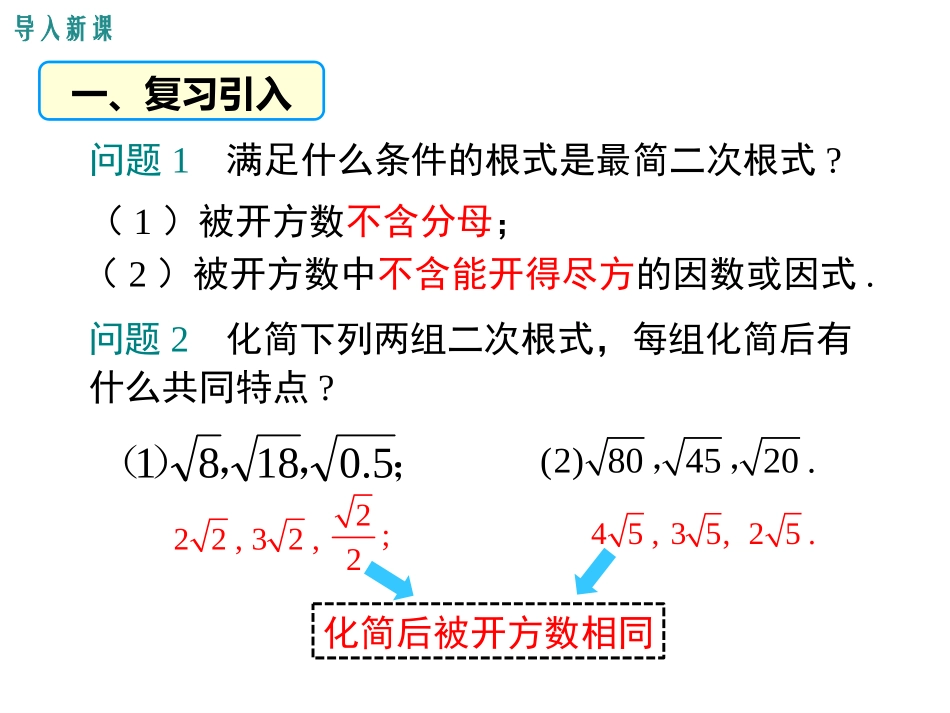
16.3二次根式的加减第十六章二次根式导入新课讲授新课当堂练习课堂小结第1课时二次根式的加减学习目标1、二次根式化简为最简二次根式以及同类二次根式的判定。2、了解二次根式的加、减运算法则。（重点）3、会用二次根式的加、减运算法则进行简单的运算。（难点）问题1满足什么条件的根式是最简二次根式?22,32,45,2;235,25.问题2化简下列两组二次根式，每组化简后有什么共同特点?（1）被开方数不含分母；（2）被开方数中不含能开得尽方的因数或因式.(2)804520.，，化简后被开方数相同导入新课一、复习引入；，，）（5.01881练一练1.下列各式中，与是同类二次根式的是（）A.B.C.D.58123D小结：几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式就叫做同类二次根式。判断同类二次根式的关键是什么？(1)化成最简二次根式，(2)被开方数相同,根指数相同(都是2)22.下列各组二次根式中是同类二次根式的是()C知识点一同类二次根式合作探究（1）（2）（3）2223与合并同类项类似,我们可以把相同二次根式的项合并.以前我们学过的整式运算的其它法则和方法也适用于二次根式的运算.5x2232=52xx23xx23x2223)4(22)23(二、二次根式的加减（化成最简二次根式）（逆用分配律）解：8+1822+322+32（）52.在有理数范围内成立的运算律，在实数范围内仍然成立.二次根式的加减实质是合并同类二次根式．整式的加减的实质是合并同类项．8+18归纳总结将二次根式化成最简二次根式，如果被开方数相同，则这样的二次根式可以合并。注意：判断几个二次根式是否可以合并，一定都要化为最简二次根式再判断。合并的方法与合并同类项类似，把根号外的因数(式)相加，根指数和被开方数(式)不变。如：manamna归纳总结二次根式的加减法法则：一般地，二次根式加减时，可以先将二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并。(1)化——将非最简二次根式的二次根式化简；加减法的运算步骤：(2)找——找出被开方数相同的二次根式；(3)并——把被开方数相同的二次根式合并。“一化简二判断三合并”知识点二二次根式的加减法法则例1计算：⑴4580解：⑴原式＝（化成______二次根式）＝（律）＝（合并）5354最简534－分配5引导学生读懂数学书课题研究成果配套课件课件制作：周恒引导学生读懂数学书课题研究成果配套课件课件制作：周恒知识点二二次根式的加减法法则例1计算：(2)aa259解：（2）原式＝＝＝aa53+a53a8计算（1）；（2）.知识点二二次根式的加减法法则767252080解：⑴原式＝＝()762－74-⑵原式＝＝＝55254+－()5124+－53知识点二二次根式的加减法法则例2计算：(1)(2)483316122532012解：⑴原式＝＝（化简二次根式）＝(合并)333632223423123234+－314知识点二二次根式的加减法法则例2计算：(2)532012解：⑵原式＝（去括号并化简）＝(合并)535232－++533+知识点二二次根式的加减法法则2、计算：（3）279818解：原式＝＝332723－+33210－知识点二二次根式的加减法法则2、计算：（4）6815.024解：原式＝＝＝()()6624222－－+6422262++－4263+知识点二二次根式的加减法法则38381、下列计算是否正确？为什么？⑴；⑵；⑶；(4).9494+=+222232222解：⑴⑵不正确，没有化简，不是同类二次根式.解：⑶正确.解：⑷不正确，2与不能合并.2