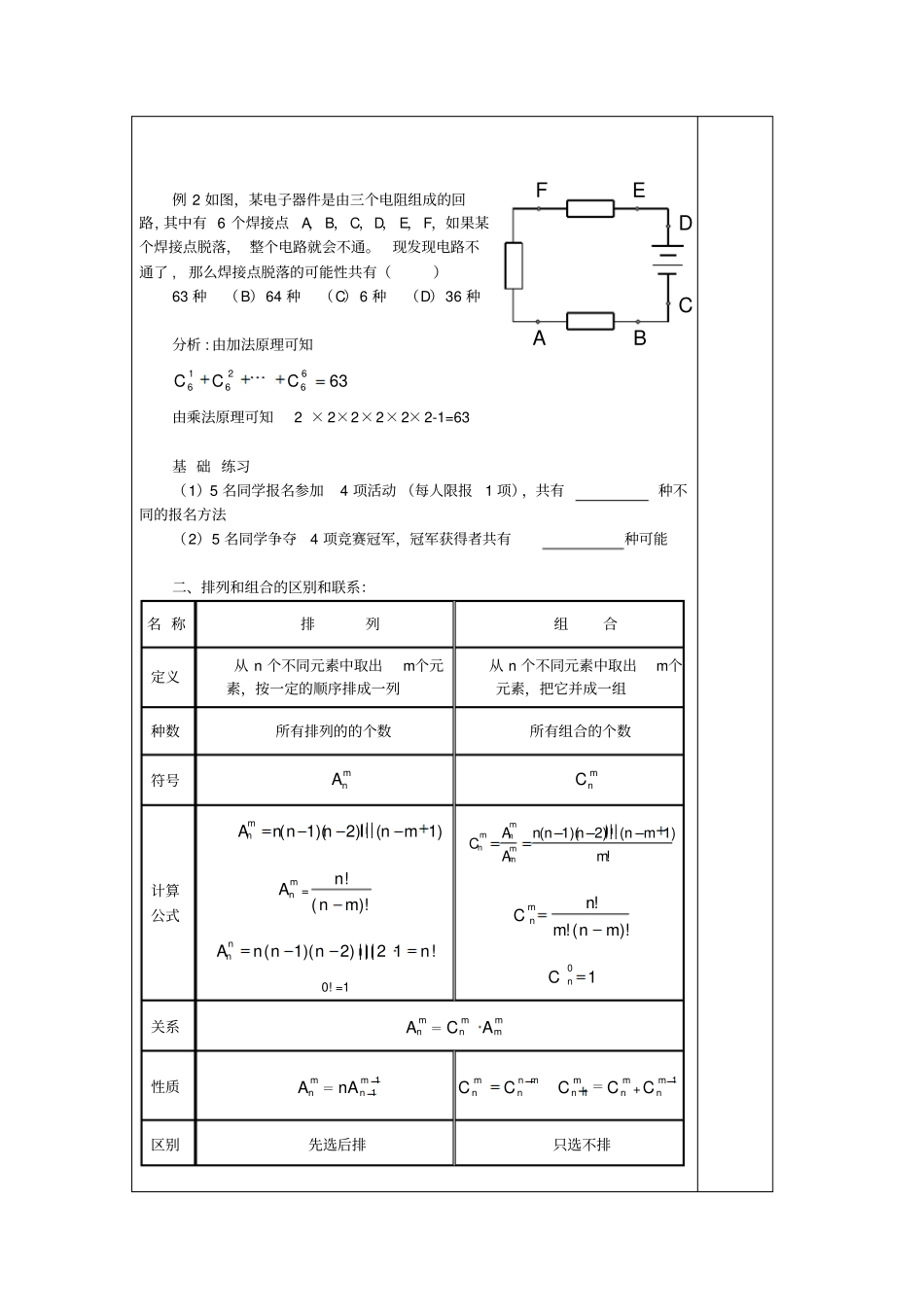
上课时间20年月日课时第课时课题排列组合、二项式定理复习课课型新课知识与技能掌握有关排列组合问题和二项式定理的基本解法,提高解决和分析问题的能力。过程与方法通过典型错误的解析,解决学生“重复”和“遗漏”等基本常见错误。情感、态度与价值观培养思维的深刻性与批判性品质。教学重点、难点1.重点:掌握有关排列组合问题和二项式定理的基本解法2.难点:有条件限制的排列组合综合问题的应用教学过程设计一、两个原理的区别与联系:名称内容分类原理分步原理定义做一件事,完成它可以有n类办法,第一类办法中有m1种不同的方法,第二类办法中有m2种不同的方法⋯,第n类办法中有mn种不同的方法,那么完成这件事共有N=m1+m2+m3+⋯mn种不同的方法做一件事,完成它可以有n个步骤,做第一步中有m1种不同的方法,做第二步中有m2种不同的方法⋯⋯,做第n步中有mn种不同的方法,那么完成这件事共有N=m1·m2·m3·⋯·mn种不同的方法.相同点做一件事或完成一项工作的方法数不同点直接(分类)完成间接(分步骤)完成例1.书架上放有3本不同的数学书,5本不同的语文书,6本不同的英语书,(1)若从这些书中任取一本,有多少种不同的选法?(2)若从这些书中取数学书、语文书、英语书各一本,有多少种不同的选法?(3)若从这些书中取不同科目的书两本,有多少种不同的选法?问题纪要CDBAEF例2如图,某电子器件是由三个电阻组成的回路,其中有6个焊接点A,B,C,D,E,F,如果某个焊接点脱落,整个电路就会不通。现发现电路不通了,那么焊接点脱落的可能性共有()63种(B)64种(C)6种(D)36种分析:由加法原理可知63662616CCC由乘法原理可知2×2×2×2×2×2-1=63基础练习(1)5名同学报名参加4项活动(每人限报1项),共有种不同的报名方法(2)5名同学争夺4项竞赛冠军,冠军获得者共有种可能二、排列和组合的区别和联系:名称排列组合定义从n个不同元素中取出m个元素,按一定的顺序排成一列从n个不同元素中取出m个元素,把它并成一组种数所有排列的的个数所有组合的个数符号mnAmnC计算公式(1)(2)(1)mnAnnnnmmnA=!()!nnm(1)(2)21!nnAnnnn0!=1(1)(2)(1)!mmnnmmAnnnnmCAm)!(!!mnmnCmn01nC关系mnA=mnCmmA性质mnA=11mnnAmnnmnCCmnC1=mnC+1mnC区别先选后排只选不排解排列组合问题遵循的一般原则:1.有序----排列;无序---组合2.分类---加法;分步---乘法3.既有分类又有分步:先分类再分步4.既有排列又有组合:先选后排5.先特殊后一般6.正难则反7.分类要不重不漏常见方法:1.优限法(一般适用于在与不在问题)2.捆绑法(一般适于相邻问题)3.插空法(一般适于不相邻问题)4.排除法(至多、至少、不都等问题)5.定序用除法练习:1.有4名男生,3名女生排成一排(1)若男生甲既不站在排头又不站在排尾,则有多少不同的排法?(2)若男生甲不站在排头,女生乙不站在排尾,则有多少不同的排法?(3)若女生全部站在一起,则有多少不同的排法?(4)若3名女生互不相邻,则有多少不同的排法?(5)若男女相间,则有多少不同的排法?(6)若有且仅有两名女生相邻,则有多少不同的排法?(7)若甲乙两人必须排在一起,丙丁两人不能排在一起,则有多少不同的排法?(8)如果3名女生不全在一起,有多少种不同的排法?(9)如果甲在乙左,丙在乙右,顺序固定,有多少种不同的排法?(1)变式:从7盆不同的盆花中选出5盆摆放在主席台前,其中有两盆花不宜摆放在正中间,则一共有_____种不同的摆放方法(用数字作答)。(2)变式1.从6人中选4人组成4×100m接力赛,其中甲不跑第一棒,乙不跑最后一棒,有多少种选法?(2)变式2:将5列车停在5条不同的轨道上,其中a列车不停在第一轨道上,b列车不停在第二轨道上,那么不同的停放方法有()(A)120种(B)96种(C)78种(D)72种(9)变式:9个人排成一排,甲、乙、丙顺序一定2.9个人排成一排(1)前排三人,中间三人,后排三人;(2)前排一人,中间二人,后排六人;三、注意区别“恰好”与“至少”例:从6双不同颜色的手套中任取4只,其中恰好有一双同色的手套的不同取法共有()(A)480种(B)240种(C)180种(D)120种练习:从6双不同颜色的手套中任取4只,其中至少有一双同色手套的不同取...