1.1.2余弦定理(1)VIP免费

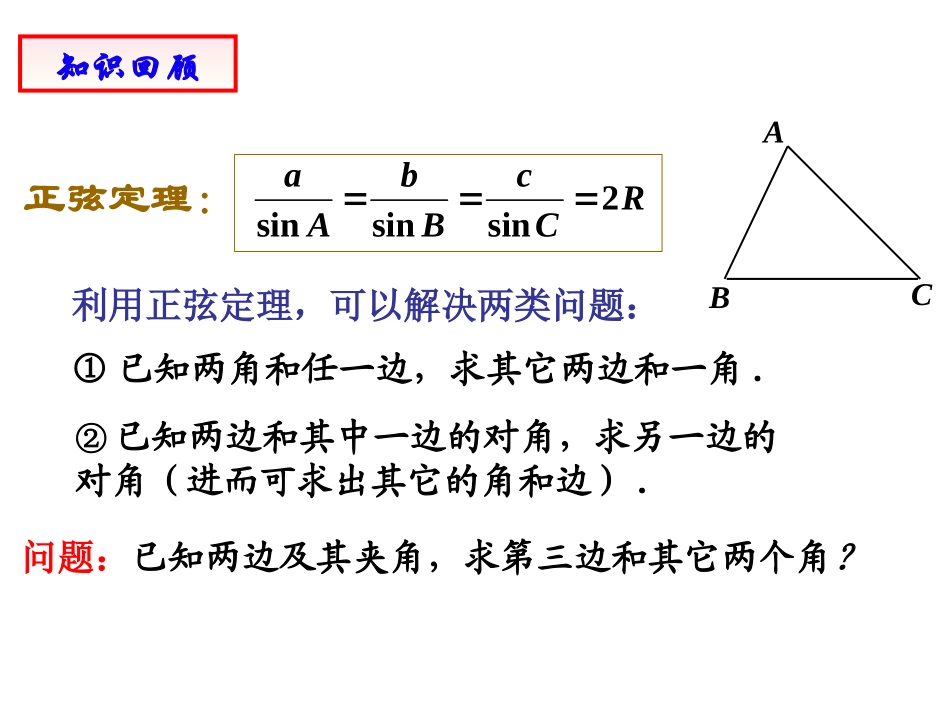
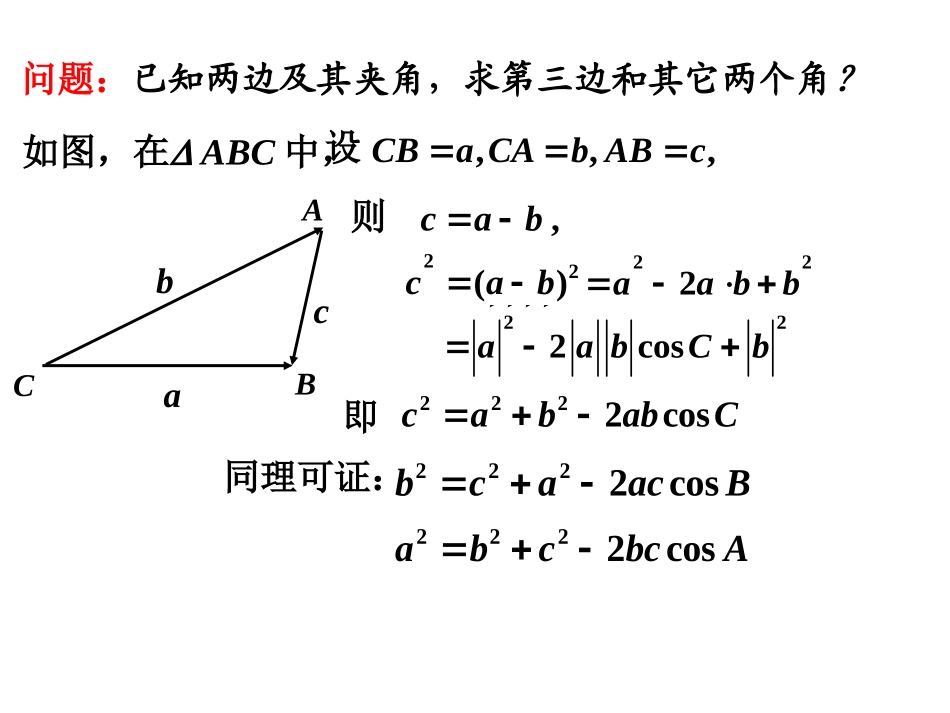
1.1.2余弦定理（1）利用正弦定理，可以解决两类问题：①已知两角和任一边，求其它两边和一角.②已知两边和其中一边的对角，求另一边的对角（进而可求出其它的角和边）.正弦定理：RCcBbAa2sinsinsin知识回顾问题：已知两边及其夹角，求第三边和其它两个角？ABC,cab22()cab222aabb2222coscababC2222cosbcaacB2222cosabcbcA问题：已知两边及其夹角，求第三边和其它两个角？如图，在ABC中，设,,,CBaCAbABc�则cbaABC222cosaabCb即同理可证：余弦定理三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍.Abccbacos2222Bacacbcos2222Cabbaccos2222bcacbA2cos222cabacB2cos222abcbaC2cos222即cbaABC由余弦定理和余弦函数的性质可知：若一个三角形两边的平方和等于第三边的平方，则第三边所对角是直角；若一个三角形两边的平方和小于第三边的平方，则第三边所对角是钝角；若一个三角形两边的平方和大于第三边的平方，则第三边所对角是锐角.（1）已知两边和它们的夹角,求第三边和其它两个角；（2）已知三边，求三个角.cbaABC利用余弦定理，可以解决两类问题：Abccbacos2222Bacacbcos2222Cabbaccos2222余弦定理：1例.15222的值边和、求角，，，中，已知在cABCbaABC解：由余弦定理Cabbaccos222215cos2222)22(222)3045cos(15cos4263482c348cbcacbA2cos222又)26(2222)26()22(22223，30A)(180CAB.13526例2在△ABC中,sinA:sinB:sinC=4:5:6,求cosA:cosB:cosC.解：由RCcBbAa2sinsinsin得a:b:c=sinA:sinB:sinC=4:5:6，可设a=4k，b=5k，c=6k，k>0，由余弦定理有bcacbA2cos222kkkkk652163625222.43同理可得，169cosB，81cosC81:169:43cos:cos:cosCBA.2:9:12ABC.4530457533的长，求，，，，中，如图，在四边形例ABADBADCBCDACBCDABCDABCD75454530解：中在ACD12030ACDADC，30CAD.3CDAC，中在CBD）（7545180CBD60由正弦定理60sin75sinCDBC60sin75sin3226，中在ABCBCABCACBCACABcos222275cos22632)226()3(225.5AB.135601410.4的长求，，，，，中，已知如图，在四边形例BCBCDBDAABADCDADABCD解：，由余弦定理，中，设在xBDABDBDAADBDADBDBAcos2222得60cos1021014222xx即096102xx)(61621舍去，解得xx16BD中，由正弦定理在BCDBCDBDCDBBCsinsin30sin135sin16BC.28课后作业2.教辅练习册第2页作业1.教材第10页习题1.1B组1，24.预习教材第11页~18页内容3.教辅第4页~6页内容.,45,2,3,.1cCABbaABC和、求已知中在4523sinsinBbaBbAa，，解法一：23245sin3sinA，1800A12060或A时，当60)1(A，75C75sin22275sin2c22622615sin215120)2(cCA，时，当.22615120cCA，，或4523cos2222BbaBacacb，，2232322cc0162cc226226cc或BbAasinsin又23sinsinbBaA12060或A2267560cCA，，解法2：.sinsin3sinsinsinsinsinsin.2CBACBACBAABC，求）（）（中，若在RCcBbAaBACBABACBA2sinsinsinsinsinsinsinsinsinsin3sinsinsin22222由正弦定理）（由条件解：abcba222.60CRbRaRcRbRa22)2()2()2(222abcbaC2cos222abab221.1sinsin43222CBACBbcacbCBABC、、，求且，，中，已知在、解：bcacbA2cos222由余弦定理，bcbc221，1800A.60A120CB1sinsin4CB1)120sin(sin4BB1)sin120coscos120(sinsin4BBB1)sin21cos23(sin4BBB1sin22sin32BBBB2cos2sin3332tanB2102302BB或CBCB且由于12012060B105B10515BB或.15)(180BAC，