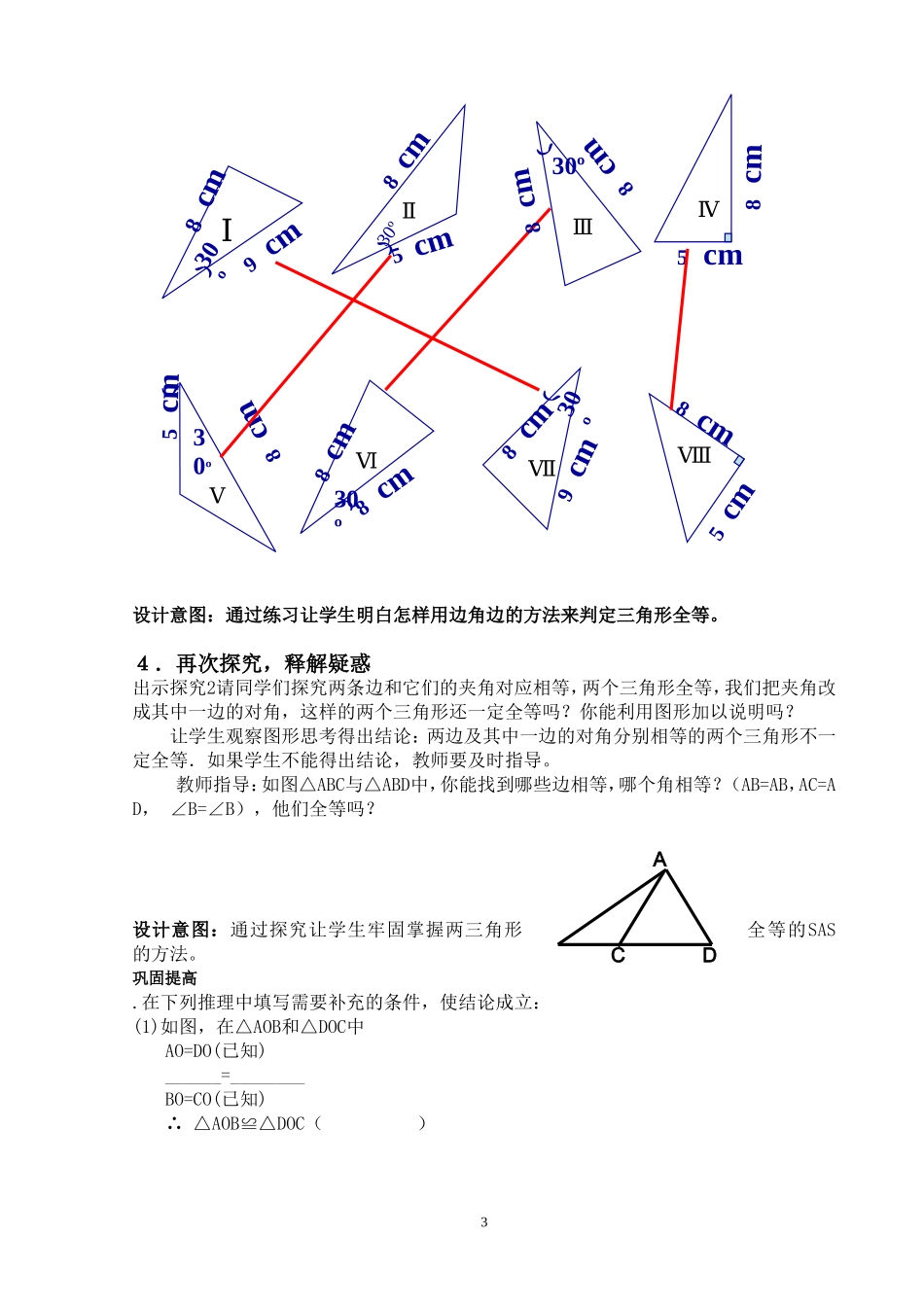
《三角形全等的判定》教学设计一、教学目标:1.理解两边和它们的夹角对应相等的两个三角形全等.2.理解两边和其中一边的对角对应相等的两个三角形不一定全等.3.经历探索三角形全等条件的过程,激发学生数学学习的兴趣.二、教学过程设计:(一)、知识回顾:引导学生回顾上节课知识,强调全等判定方法的基本格式.三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。用数学语言表述:在△ABC和△DEF中AB=DEBC=EFCA=FD∴△ABC≌△DEF(SSS)(二)、创设情境,引入课题1.问题情景:有一池塘,因施工需要要在池塘两侧AB处各埋设一根电线杆,因无法直接量出A、B两点的距离,用什么办法才能测出A、B两端之间的距离呢?学会本节课的内容你们将轻松的解决这个问题。2.:已知任意△ABC,画△A'B'C',使A'B'=AB,A'C'=AC,∠A'=∠A.(及两边和它们的夹角分别相等)。把画好的图形剪下来,放到△ABC上,它们全等吗?让学生先独立思考,然后小组内交流,老师根据学生画的情况及时点拨。学生的画法可能不同,只要求画出图形不写画法。设计意图:从实际问题出发激发学生的求知欲望让学生明白数学知识来源于生活。探究活动1培养学生的动手能力和归纳问题的能力。(三)、交流对话,探求新知1.根据前面的操作,鼓励学生用自己的语言来总结规律:两边和它们的夹角分别相等的两个三角形全等.(SAS,边角边)2.出示问题锻炼学生运用能力:(1).考考你:已知:如图,AB=CB,∠ABD=∠CBD,△ABD和△CBD全等吗?(2).问题推广:已知:如图,AB=CB,∠ABD=∠CBD。问AD=CD吗?DB平分∠ADC吗锻炼学生运用能力:3.回顾问题情景,解决实际问题:有一池塘,因施工需要要在池塘两侧A、B处各埋设一根电线杆,因无法直接量出A、B两点的距离,用什么办法才能测出A、B两端之间的距离呢?1BCADABCDFE小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使DC=AC,连结BC并延长至E点,使EC=BC,连结DE,用米尺测出DE的长,这个长度就等于A,B两点的距离。你能说明他这样做的理由吗?(若学生不能顺利得到证明思路,教师也可作如下分析:要想证AB=DE,只需证△ABC≌△DEC△ABC与△DEC全等的条件现有……还需要……)明确证明分别属于两个三角形的线段相等或者角相等的问题,常常通过证明这两个三角形全等来解决.设计意图:让学生明白数学知识来源于生活并服务于生活,提高学生的学习兴趣。尝试应用1.填空:如图3,已知AD∥BC,AD=CB,要用边角边公理证明△ABC≌△CDA,需要三个条件,这三个条件中,已具有两个条件,一是AD=CB(已知),二是___________;还需要一个条件_____________(这个条件可以证得吗?2.在下列图中找出全等三角形2设计意图:通过练习让学生明白怎样用边角边的方法来判定三角形全等。4.再次探究,释解疑惑出示探究2请同学们探究两条边和它们的夹角对应相等,两个三角形全等,我们把夹角改成其中一边的对角,这样的两个三角形还一定全等吗?你能利用图形加以说明吗?让学生观察图形思考得出结论:两边及其中一边的对角分别相等的两个三角形不一定全等.如果学生不能得出结论,教师要及时指导。教师指导:如图△ABC与△ABD中,你能找到哪些边相等,哪个角相等?(AB=AB,AC=AD,∠B=∠B),他们全等吗?设计意图:通过探究让学生牢固掌握两三角形全等的SAS的方法。巩固提高.在下列推理中填写需要补充的条件,使结论成立:(1)如图,在△AOB和△DOC中AO=DO(已知)______=________BO=CO(已知)∴△AOB≌△DOC()ر5cmⅠر30º8cm9cmⅥر30º8cm8cmⅣⅣ8cm5cmⅡ30ºر8cm5cmⅤ30º8cmⅧ8cm5cmر30º8cm9cmⅦⅢر30º8cm8cmⅢ3ACD2.已知:如图:AC=AD,∠CAB=∠DAB.求证:△ACB≌△ADB.证明:△ACB≌△ADB这两个条件够吗?设计意图:通过练习培养学生合作能力灵活应用知识的能力总结证明三角形全等的步骤1写出在哪两个三角形中证明全等。(注意把表示对应顶点的字母写在对应的位置上).2.按边、角、边的顺序列出三个条件,用大括号合在一起.3.证明全等后要有推理的依据练习:已知:如图,AB=ACAD=AE.求证:△ABE≌△ACD.证明:在△ABE和△ACD...