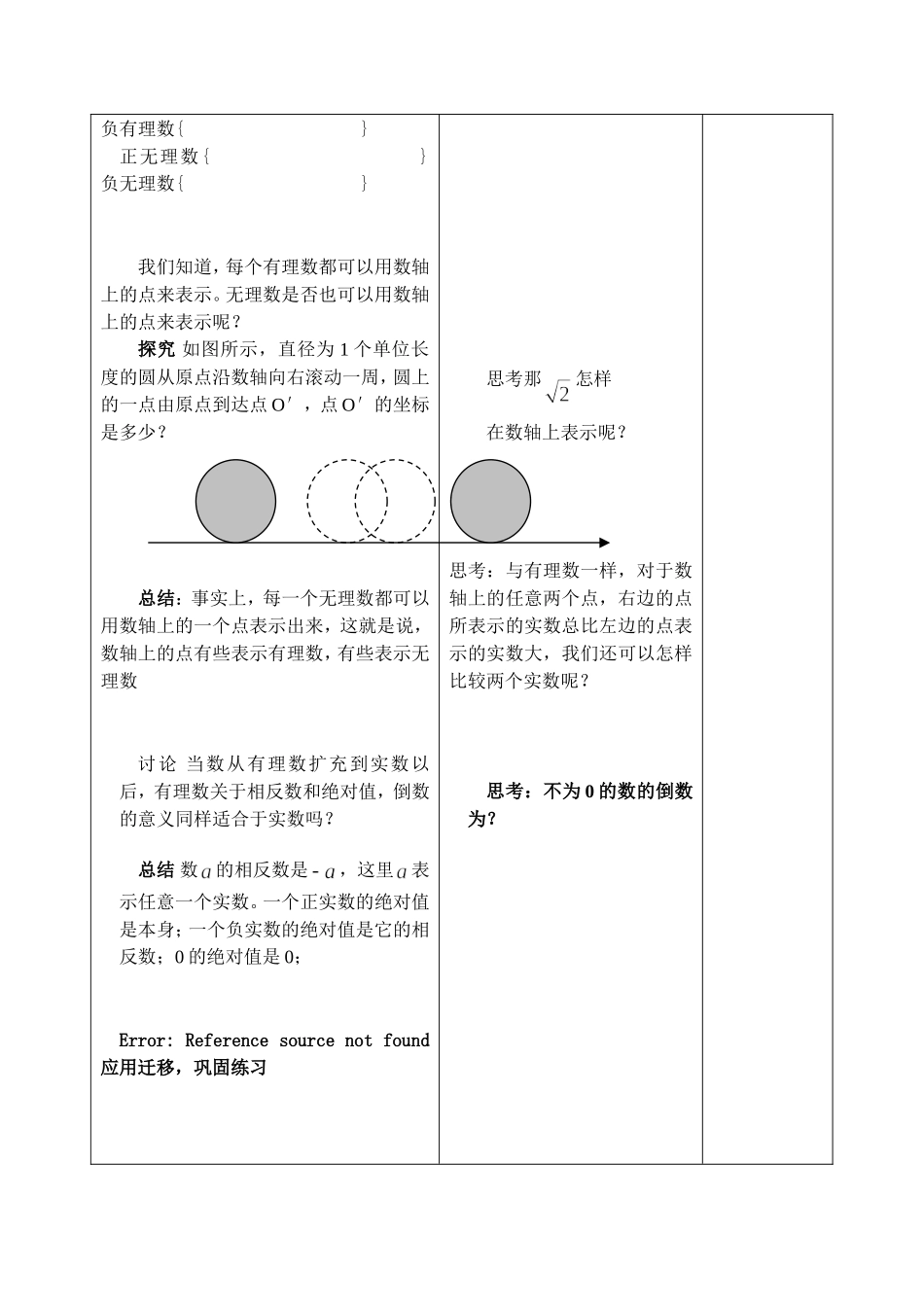
“学程导航”课时教学计划施教日期年月日教学内容13.3实数共几课时2课型新授第几课时1教学目标1.了解无理数和实数的概念,知道实数和数轴上的点一一对应,能估算无理数的大小2.了解分类的标准与分类结果的相关性,进一步了解体会“集合”的含义教学重难点教学重点:实数的意义和实数的分类;教学难点:体会数轴上的点与实数是一一对应的教学资源预习设计预习提纲:1.看书本P82-84,思考无理数可以在数轴上表示吗?2.怎样来比较两个无理数的大小尝试练习:1.完成书本P86后的练习1.22.通过理解书本中的知识完成学程导航的请你思考部分学程预设导学策略调整与反思一.合作交流,解读探究探究使用计算器计算,把下列有理数写成小数的形式,你有什么发现?3,,,,,归纳任何一个有理数都可以写成有限小数或无限循环小数的形式。反过来,任何有限小数或无限循环小数也都是有理数无限不循环小数又叫无理数,也是无理数结论有理数和无理数统称为实数试一试把实数分类你能举出一些无理数来吗?把下列各数分别填入相应的集合里:正有理数{}我们发现,上面的有理数都可以写成有限小数或者无限循环小数的形式,即,,,,,引入实数的第二种按照性质的分法负有理数{}正无理数{}负无理数{}我们知道,每个有理数都可以用数轴上的点来表示。无理数是否也可以用数轴上的点来表示呢?探究如图所示,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O′,点O′的坐标是多少?总结:事实上,每一个无理数都可以用数轴上的一个点表示出来,这就是说,数轴上的点有些表示有理数,有些表示无理数讨论当数从有理数扩充到实数以后,有理数关于相反数和绝对值,倒数的意义同样适合于实数吗?总结数的相反数是,这里表示任意一个实数。一个正实数的绝对值是本身;一个负实数的绝对值是它的相反数;0的绝对值是0;Error:Referencesourcenotfound应用迁移,巩固练习思考那怎样在数轴上表示呢?思考:与有理数一样,对于数轴上的任意两个点,右边的点所表示的实数总比左边的点表示的实数大,我们还可以怎样比较两个实数呢?思考:不为0的数的倒数为?学程预设导学策略调整与反思(1)的相反数是,的相反数是(2)让学生思考P86的第一题Error:Referencesourcenotfound总结反思作业设计1.完成P86-87的1.3.62.学程导航以及自主检测中的实数(一)“学程导航”课时教学计划施教日期年月日教学内容13.3实数共几课时2课型新授第几课时2教学目标1.知道实数与数轴上的点一一对应,有序实数对与平面上的点一一对应2.了解在有理数范围内的运算及运算法则,运算性质等在实数范围内仍然成立,能熟练的进行实数运算,在实数运算时,根据问题的要求取近似值,转化为有理数进行计算教学重难点教学重点:实数范围内的运算教学难点:无理数的加减乘除运算教学资源预习设计预习提纲:预习书本P85思考实数范围内的五个运算律尝试练习:1。完成书本P86的练习3.42。完成学程导航的请你思考学程预设导学策略调整与反思Error:Referencesourcenotfound创设情景,导入新课Error:Referencesourcenotfound合作交流,解读探究自主探索独立阅读,自习教材讨论下列各式错在哪里?1、2、3、4、当时,例一.计算下列各式的值:Error:ReferencesourcenotfoundError:Referencesourcenotfound总结实数范围内的运算方法及运算顺序与在有理数范围内都是一样的【练一练】计算Error:Referencesourcenotfound(2)试一试计算:(精确到0.01)·(结果保留3个有效数字)(3)求5的算术平方根与3的平方根之和复习导入:1、用字母来表示有理数的乘法交换律、乘法结合律、乘法分配律2、用字母表示有理数的加法交换律和结合律这里用到的运算律有哪些?总结在实数运算中,当遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数,再进行计算(保留3位有效数字)Error:Referencesourcenotfound应用迁移,巩固提高例1为何值时,下列各式有意义?例2计算(1)(精确到0.01)(2)()(精确到0.01)例3计算Error:Referencesourcenotfound总结反思Error:Referencesourcenotfound课堂跟踪反馈1...