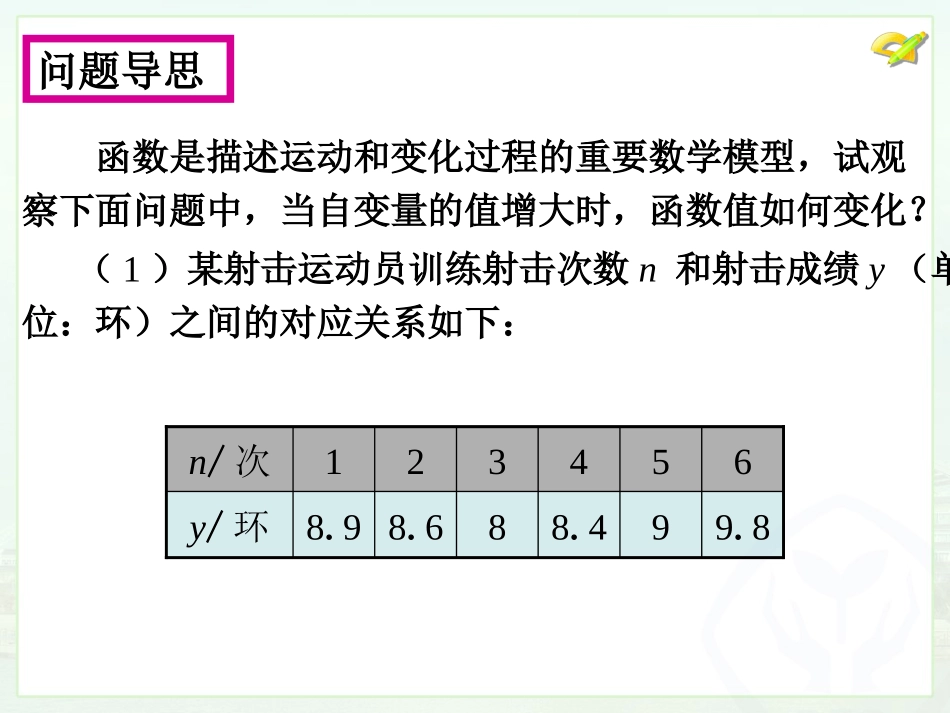
八年级下册19.1.2函数的图象(1)函数是描述运动和变化过程的重要数学模型,试观察下面问题中,当自变量的值增大时,函数值如何变化?(1)某射击运动员训练射击次数n和射击成绩y(单位:环)之间的对应关系如下:n/次123456y/环8.98.688.499.8问题导思(2)下图是北京市某天24小时内气温的变化图,气温T随时间t的变化而变化.函数是描述运动和变化过程的重要数学模型,试观察下面问题中,当自变量的值增大时,函数值如何变化?问题导思函数是描述运动和变化过程的重要数学模型,试观察下面问题中,当自变量的值增大时,函数值如何变化?22=-.yxx(3)上述3个问题中,你能观察到当自变量增大时,函数值是怎样变化的吗?问题导思(2)最清楚;(3)最不清楚.上述3个问题中,函数值随自变量的增大的变化规律,哪一个最清楚,哪一个最不清楚?为什么?问题导思41424t/小时8T/℃0气温曲线是用图象表示函数的一个实际例子。函数的图象是由直角坐标系中的一系列点组成.正方形的边长为x,面积为S。面积s不是边长x的函数?它们的函数关系式怎样表示?面积s与边长x的函数关系式为:s=x2(x>0)能不能用图象直观的反映出来呢?思考:(1)这个函数的自变量取值范围是什么?(2)怎样获得组成曲线的点?(3)怎样确定满足函数关系的点的坐标?(4)自变量x的一个确定的值与它所对应的唯一的函数值S,是否唯一确定了一个点(x,S)呢?探究S=x2(x>0)x00.511.522.53s00.2512.2546.2591、列表:2、描点:3、连线:xs012345-1-2-3-4-512345-1用空心圈表示不在曲线的点用平滑曲线去连接画出的点画图:一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.例题导练:例1下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.825285868x/min0.80.6y/kmO根据图象回答下列问题:(1)食堂离小明家多远?小明从家到食堂用了多少时间?应用例1下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图象回答下列问题:(2)小明在食堂吃早餐用了多少时间?825285868x/min0.80.6y/kmO应用例1下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图象回答下列问题:(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?825285868x/min0.80.6y/kmO应用例1下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图象回答下列问题:(4)小明读报用了多长时间?825285868x/min0.80.6y/kmO应用例1下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图象回答下列问题:(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?825285868x/min0.80.6y/kmO八年级(2)班从学校出发去某景点旅游,全班分成甲、乙两组.甲组乘坐大客车,乙组乘坐小轿车.已知甲组比乙组先出发,汽车行驶的路程s(单位:km)和行驶时间t(单位:min)之间的函数关系如图所示:应用1020304050607055s/kmt/minO乙甲给出下列说法:①学校到景点的路程为55km;②甲组在途中停留了5min;③甲、乙两组同时到达景点;④相遇后,乙组的速度小于甲组的速度.根据图象信息,以上说法正确的有.①②拓展从图象中还能获得哪些信息?应用1020304050607055s/kmt/minO乙甲(1)函数图象上点的横坐标和纵坐标分别表示什么?(2)画函数图象时,能画出满足函数关系的所有的点吗?(3)你认为观察函数图象时要注意哪些问题?课堂小结图象信息(形)图象上点的坐标特点(数)对应关系和变化规律作业:教科书第82页第8题;教科书第83页第9题.课后作业