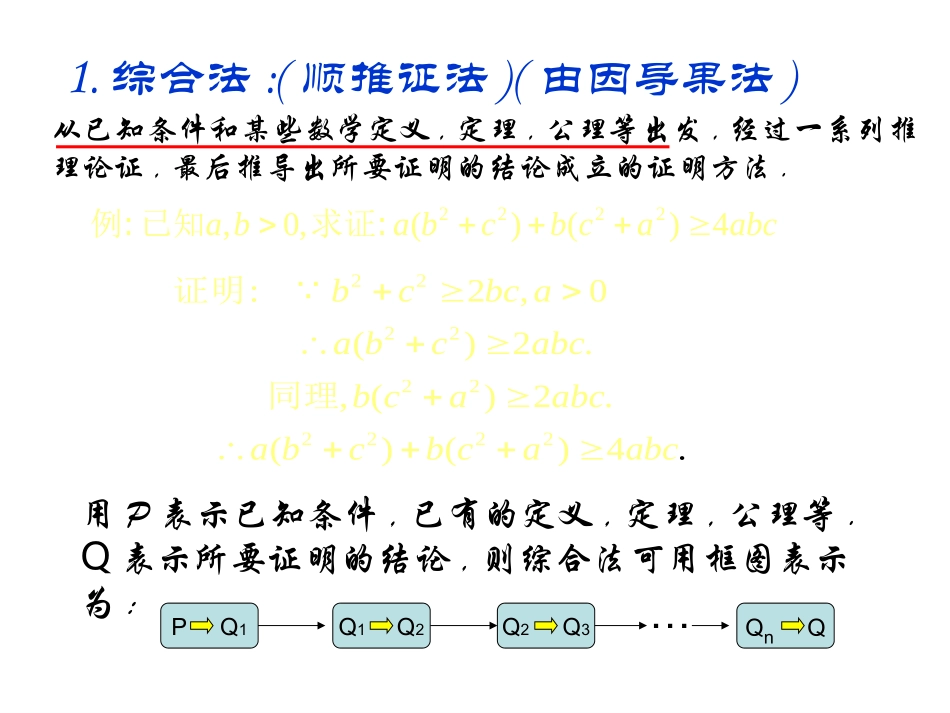
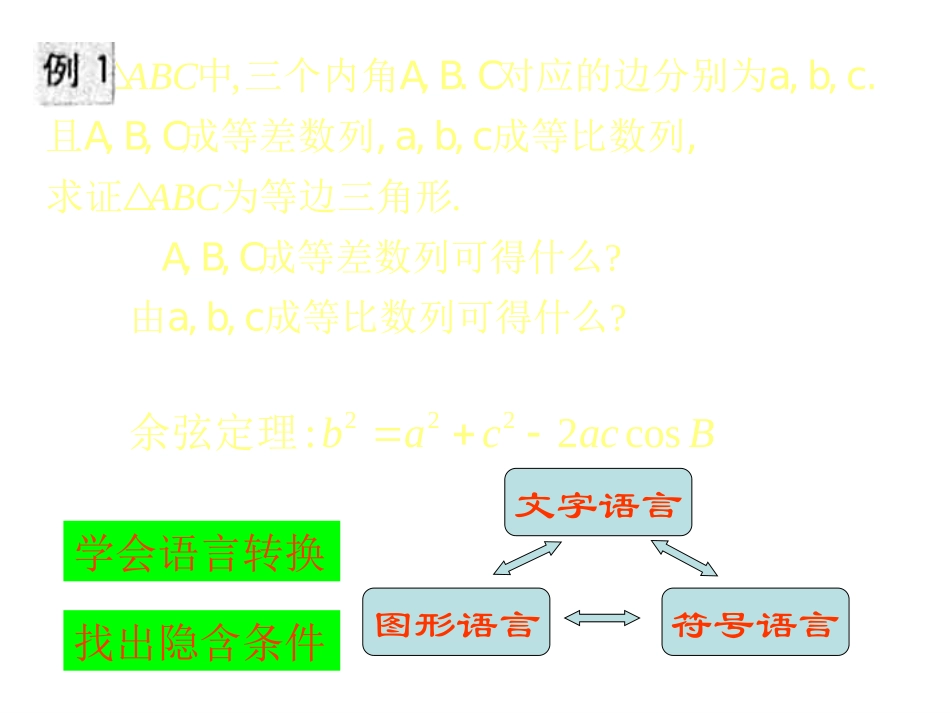
1.综合法:(顺推证法)(由因导果法)从已知条件和某些数学定义,定理,公理等出发,经过一系列推理论证,最后推导出所要证明的结论成立的证明方法.2222,0,()()4ababcbcaabc例:已知求证:2222222222:2,0()2.,()2..()()4bcbcaabcabcbcaabcabcbcaabc证明同理PQ1QnQQ2Q3Q1Q2…用P表示已知条件,已有的定义,定理,公理等.Q表示所要证明的结论,则综合法可用框图表示为:?:?A,B,C成等差数列可得什么由a,b,c成等比数分由列可得什么析0260(?)ACBB为什么2bac?怎样把边,角联系起来222:2cosbacacB余弦定理符号语言图形语言文字语言学会语言转换找出隐含条件3,.ABCABC例中三个内角A,B.C对应的边分别为a,b,c.且A,B,C成等差数列,a,b,c成等比数列,求证为等边三角形练习:求证:5321232log19log19log19证明:因为1loglogabba所以左式=log195+2log193+3log192=log19(5×32×23)=log19360.因为log19360
abc+abc+abc=a+b+c.法1:∵a、b、c不相等正,且abc=1,111∴++=bc+ca+ababc证为数例.已知a、b、c不相等正,且abc=1,111求:a+b+c<++.abc为数证.111∴a+b+c<++成立abc一.综合法111111+++bccaab<++222111=++.abc法2:∵a、b、c不相等正,且abc=1,111∴a+b+c=++bccaab证为数.111∴a+b+c<++成立abc例.已知a、b、c不相等正,且abc=1,111求:a+b+c<++.abc为数证2.分析法.(逆推证法)(执果索因法)从证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知,定理,定义,公理等).这种证明的方法叫做分析法.:.2abab证明不等式:例如:,2abab证要证明2abab只需证0只需证a+b-2ab2)0b只需证(a此式显然成立,因此原不等式立.用Q表示所要证明的结论,则分析法可用框图表示为:得到一个明显成立的条件QP1P1P2P2P3…例2.求证:3725证明:因为都是正数,3725和所以为了证明3725只需证明22(37)(25)展开得1022120即215只需证明21<25,因为21<25成立,所以不等式成立。3725分析法证明的逻辑关系是:B(结论)B1B2…BnA(已知).在分析法证明中,从结论出发的每一个步骤所得到的判断都是结论成立的充分条件,最后一步归结到已被证明的事实。因此从最后一步可以倒推回去,直到结论,但这个倒推过程可以省略。用P表示已知条件,定义,定理,公理等,用Q表示要证的结论,则上述过程可用框图表示为:……PP1P1P2Pn-1PnQm-1QmQQ1Q1Q2:例已知a>5,求:a-5-a-3