正弦函数的性质与图像VIP免费

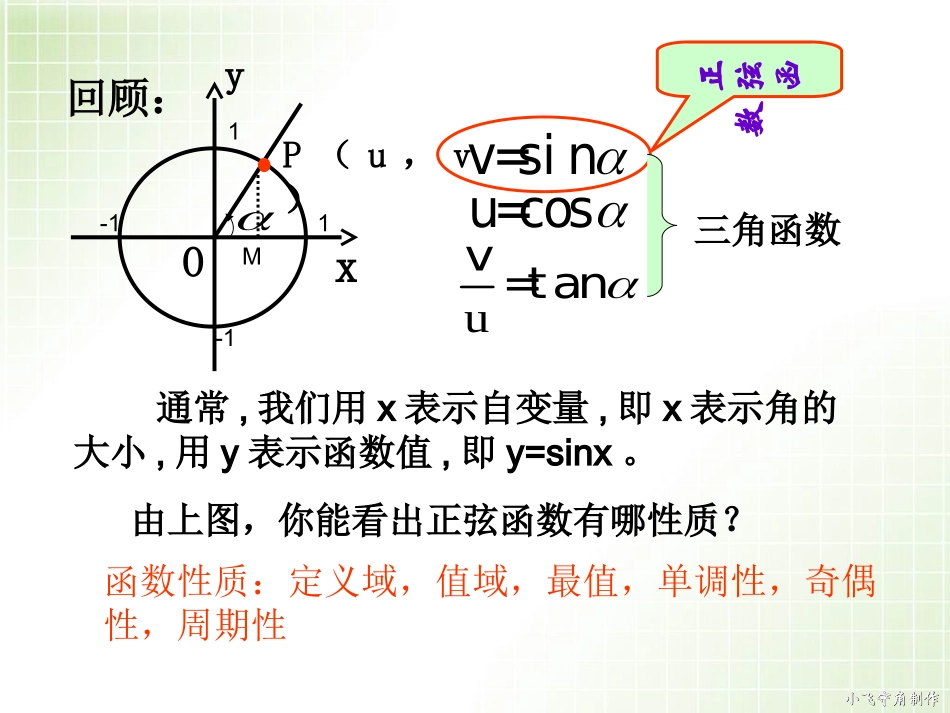
小飞守角制作小飞守角制作正弦函数u=cosuv=tan由上图，你能看出正弦函数有哪性质？通常,我们用x表示自变量,即x表示角的大小,用y表示函数值,即y=sinx。回顾：P（u，v）Oxy-1-111Mv=sin三角函数函数性质：定义域，值域，最值，单调性，奇偶性，周期性小飞守角制作小飞守角制作根据正弦函数y=sinx的定义，我们不难从单位圆看出正弦函数y=sinx有以下性质：1.定义域是全体实数；2.最大值是1,最小值是-1,值'''域是[-1,1];3.它是周期函数，其周期是2π;一.正弦函数的性质4.在[0,2π]上的单调性为：在[0,π/2]上是增加的；在[π/2,π]上是减少的；在[π,3π/2]上是减少的；在[3π/2,2π]上是增加的；POxy-1-1x11My=sinx5.y=sinx是奇函数。小飞守角制作小飞守角制作在画正弦函数图像时,我们可以先画出上的正弦函数的图像,再利用周期性将其延拓到整个定义域上.二.正弦函数的图像0,2,Ⅰ、用描点法作出函数图象⑴.列表⑵.描点⑶.连线sin,0,2yxxxy63232656734233561120212301212321230021231---223xy0211---小飞守角制作小飞守角制作rhOAPM)b,a(设任意角的终边与单位圆交于点P，过点p做x轴的垂线，垂足M，称线段MP为角的正弦线。正弦线的概念:正弦线是有向线段，是由M指向P的，P称为正弦线的终点。C:\Users\Administrator\Desktop\正弦函数ok\正弦线.swf小飞守角制作小飞守角制作).67sin,67(),6sin6(，用单位圆中正弦线表示正弦的方法,作出点PM)6sin6(1，PO1yXAo6PP67H6267)67sin67(1，H小飞守角制作小飞守角制作o1A...........1-1函数y=sinx,x[0,2]3/2/2o2xy描图：用光滑曲线将这些正弦线的终点连结起来Ⅱ、用正弦线作出函数图象单位圆分成12等份，每一份多少弧度？6小飞守角制作小飞守角制作2oxy---11--13232656734233561126sin[0,2]yxx在函数的图象上，起关键作用的点有：sin,[0,2]yxx最高点：最低点：与x轴的交点：(0,0)(,0)(2,0))1,(23)1,2(在精度要求不高的情况下，我们可以利用这5个点画出函数的简图，一般把这种画图方法叫“五点法画图”。小飞守角制作小飞守角制作.....五点法作函数的简图])2,0[(sinxxy坐标依次为：（0，0）、（，1）、（，0）、（，-1）、（，0）2232Ⅲ、五点作图法xyo-2-234······-11小飞守角制作小飞守角制作正弦函数的图象x6yo--12345-2-3-41y=sinxx[0,2]y=sinxxR正弦曲线yxo1-122322小飞守角制作小飞守角制作三、例题讲解例1：用五点法画出函数的简图y=1+sinx,x[0∈，2π]。分析：利用五点法画正弦函数y=sinx的图像,五个关键点是：=========(0,0),(/2,1),(,0),(3/2,-1),(2,0)，而本题的函数是y=1+sinx，它的图像和y=sinx的图像形状是一样的，只是向上平移了一个单位，所以还是取对应的这五点，只不过是纵坐标发生了变化，横坐标并没有变。解:按关键五点列表o122yx20-10100x2sinx1sinx3211012小飞守角制作小飞守角制作变式：画出函数的简图。sin,[0,2]yxx20100-10100x2sinxsinx0-132解:按关键五点列表ox122y小飞守角制作小飞守角制作1.利用单位圆中的正弦线画出正弦函数的图象——几何法优、缺点:画图准确但较繁琐。2.用五个关键点(与x轴的交点、曲线最高点及最低点）画图——五点法优、缺点：画图简捷但不够准确。八.课堂小结:小飞守角制作小飞守角制作（1）作直角坐标系，在直角坐标系的y轴左侧画单位圆，圆心在x轴上．（3）找横坐标：把x轴上从0到2这一段分成12等份；（2）把单位圆分成12等份。过单位圆上的各分点作x轴的垂线，可以得到对应于各角的正弦线；（4）找纵坐标：将正弦线对应平移，即可作出相应12个点；用正弦线作正弦函数的图象])2,0[(sinxxy（5）连线：用平滑的曲线将12个点依次从左到右连接起来，即得到的图象。])2,0[(sinxxy四、几何法作图演示做图