二次函数y=ax2-的图象和性质VIP免费

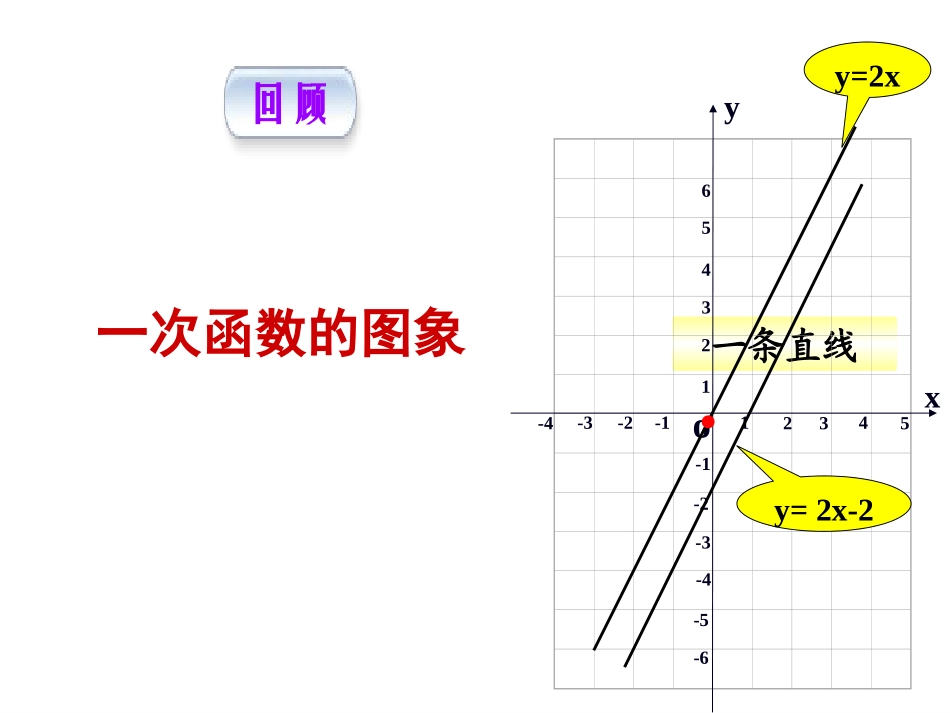
二次函数y=ax2的图象和性质回顾一次函数的图象一条直线yo12345-1-2-3-4-5-6213456-1-2-3-4xy=2x·y=2x-2（1）列表：在x的取值范围内列出函数对应值表描点法2yx画二次函数的图象.探究二次函数的图象是什么样子的？(2)描点：在坐标平面上描出点（3)连线：用平滑的曲线连接起来x…-3-2-10123…y画函数y=x2的图像解:(1)列表…9410149…(2)描点(3)连线12345x12345678910yo-1-2-3-4-5根据表中x,y的数值在坐标平面中描点(x,y),再用平滑曲线顺次连接各点,就得到y=x2的图像.y=x2画二次函数的图象。2yx解：（1）列表：在x的取值范围内列出函数对应值表：……y…3210-1-2-3…x-9-9-4-4-1-10描点法探究（2）在平面直角坐标系中描点：xyo-4-3-2-11234-2-4-6-8y=-x2（3）用光滑曲线顺次连接各点，便得到函数y=-x2的图象.-10抛物线：像这样的曲线通常叫做抛物.二次函数的图象都是抛物线.一般地，二次函数的图象叫做抛物线.2yaxbxc2yaxbxc仔细观察仔细观察2xy2xytx()=x×xux()=2×x×x2.描点：3.连线：xy=2x2-201-12y=x2y=x212……顶点坐标y=x2y=2x2y=x212探究………………1.列表：画出函数y=x2、y=2x2、y=x2的图象：12410148202820.500.52f1x()=-2×x×xg1x()=-12×x×x2.描点：3.连线：xy=-2x2-201-12y=-x2y=-x212……顶点坐标y=-x2y=-2x2y=-x212y=x2y=2x2y=x212………………1.列表：画出函数y=-x2、y=-2x2、y=-x2的图象：12－4－10－1－4－8－20－2－8－2－0.50－0.5－2开口大小抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2(a>0)y=ax2(a<0)原点（0，0）原点（0，0）y轴y轴在x轴的上方(除顶点外)在x轴的下方(除顶点外)向上向下当x=0时,y最小值为0.当x=0时,y最大值为0.在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.越小,开口越大.越大,开口越小.aa归纳.总结归纳.总结课堂小结形如（a、b、c是常数，a≠0）的函数叫做x的二次函数，a叫做二次函数的系数，b叫做一次项的系数，c叫作常数项。2yaxbxc1.二次函数：2、抛物线：二次函数的图象都是抛物线。2xy2xy一般地，抛物线y=ax2的对称轴是____轴，顶点是_______.当a>0时，抛物线的开口向__，顶点是抛物线的________，a越大，抛物线的开口越___;当a<0时，抛物线的开口向____，顶点是抛物线的最____点，a越大，抛物线的开口越____.y原点最低点上小下高大3、抛物线y=ax2的图象：4、抛物线y=ax2的图象中a决定开口方向和形状。a相同开口方向相同、形状相同，|a|越大，开口越小。练习：P32作业:P41(3.4两题)