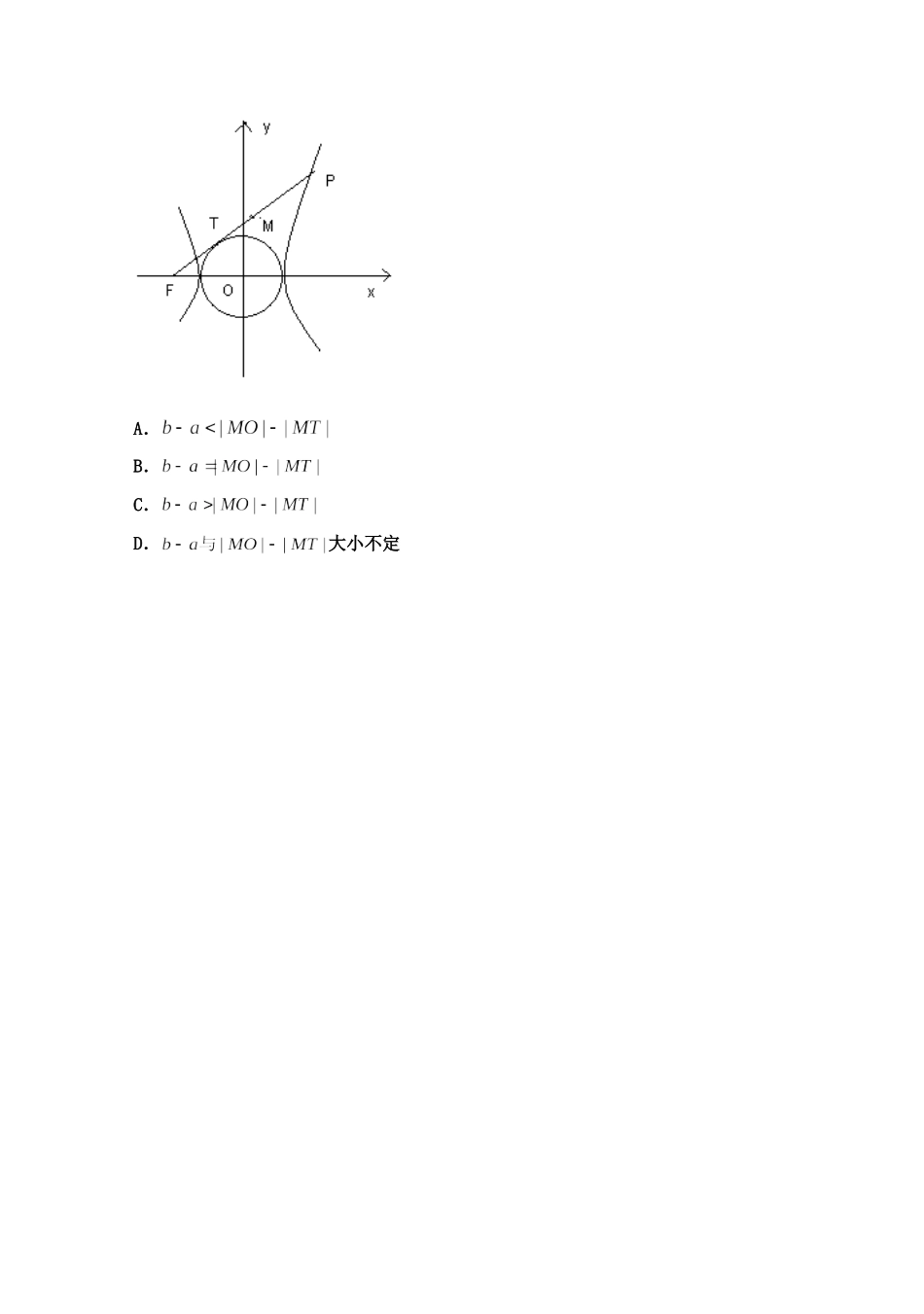
乐山一中2012-2013学年高二第一阶段考试数学试题第I卷选择题(共60分)一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.抛物线的焦点坐标是A.(1,0)B.(0,1)C.(0,2)D.(2,0)2.若椭圆长轴长为8,且焦点为F1(-2,0),F2(2,0),则这个椭圆的离心率等于A.B.C.D.3.已知方程表示双曲线,则m的取值范围是A.m<-2B.m>-1C.-2-14.以双曲线1322xy的一个焦点为圆心,离心率为半径的圆的方程是A.4)2(22yxB.2)2(22yxC.2)2(22yxD.4)2(22yx5.如果点M(x,y)在运动过程中,总满足关系式则点M的轨迹方程为A.B.C.D.6.已知双曲线C:-=1的焦距为10,点P(2,1)在C的渐近线上,则C的方程为A.-=1B.-=1C.-=1D.-=17.抛物线上有一点M,它的横坐标为3,它到焦点的距离是5,则抛物线的方程为A.B.C.D.8.已知F1、F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=A.B.C.D.9.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线xy162的准线交于,AB两点,43AB,则C的实轴长为A.2B.22C.D.10.已知定点A(3,4),点P为抛物线y2=4x上一动点,点P到直线x=-1的距离为d,则|PA|+d的最小值为A.B.2C.D.11.设椭圆的离心率,右焦点F(c,0),方程的两个根分别为x1,x2,则点P(x1,x2)在A.圆内B.圆上C.圆外D.以上三种情况都有可能12.(文科)已知双曲线与双曲线,设连结它们的顶点构成的四边形的面积为,连结它们的焦点构成的四边形的面积为,则的最大值为A.B.C.4D.2(理科)过双曲线的左焦点F,作圆的切线交双曲线右支于点P,切点为T,PF的中点M在第一象限,则以下正确的是A.B.C.D.大小不定第II卷非选择题(90分)二.填空题:(本大题共4小题,每小题4分,共16分)13.双曲线的两条渐近线互相垂直,那么双曲线的离心率为14.已知B,C是两个定点,坐标分别为(3,0),(-3,0),若顶点A的轨迹方程为,则△ABC的周长为15.过抛物线的焦点作一条直线交抛物线于A(x1,y1),B(x2,y2),则的值为16.方程所表示的曲线为C,有下列命题:①若曲线C为椭圆,则24或t<2;③曲线C不可能为圆;④若曲线C表示焦点在y轴上的双曲线,则t>4.以上命题正确的是(填上所有正确命题的序号)。三.解答题:(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)求双曲线的实轴长,虚轴长,顶点和焦点的坐标,离心率,渐近线方程。18.(本小题满分12分)(1)已知椭圆的中心在原点,一个焦点为F(,0),且长轴长是短轴长的2倍,求该椭圆的标准方程;(2)求与椭圆有共同焦点,且经过点(2,-5)的双曲线的标准方程。19.(本小题满分12分)已知平面内一动点P到定点F与到定直线x=的距离相等.(1)求动点P的轨迹方程(2)若直线y=x-2与动点P的轨迹相交于A,B两点,求△AOB的面积(O为坐标原点)20.(本小题满分12分)矩形ABCD的两条对角线相交于点(20)M,,AB边所在直线的方程为360xy,点(11)T,在AD边所在直线上。(1)求AD边所在直线的方程;(2)求矩形ABCD外接圆的方程;(3)若动圆P过点(20)N,,且与矩形ABCD的外接圆外切,求动圆P的圆心的轨迹方程。21.(本小题满分12分)(12分)给定椭圆,称圆心在坐标原点,半径为的圆是椭圆的“伴随圆”。若椭圆C的一个焦点为,其短轴上的一个端点到距离为。(1)求椭圆及其“伴随圆”的方程;(2)若过点的直线与椭圆C只有一个公共点,且截椭圆C的“伴随圆”所得的弦长为,求的值。22.(本小题满分14分)在平面直角坐标系中,为坐标原点,给定两点,,点C满足,其中且。(1)求点C的轨迹方程;(2)设点C的轨迹与双曲线(且)交于M、N两点,且以MN为直径的圆过原点,求证:为定值;(3)(理科做,文科不做)在(2)的条件下,若双曲线的离心率不大于,求双曲线实轴长的取值范围。