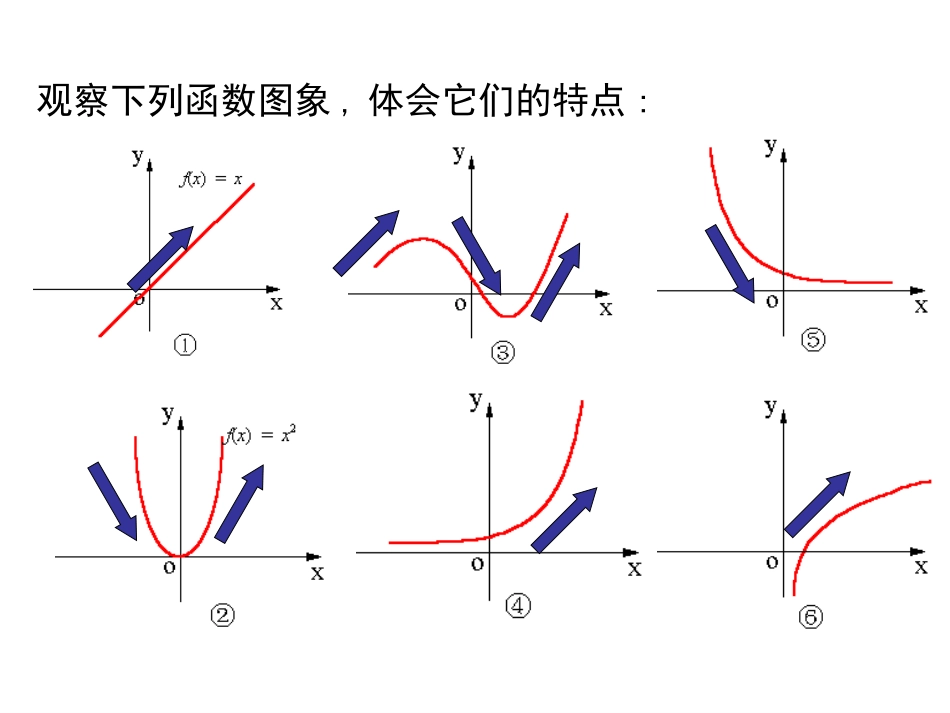
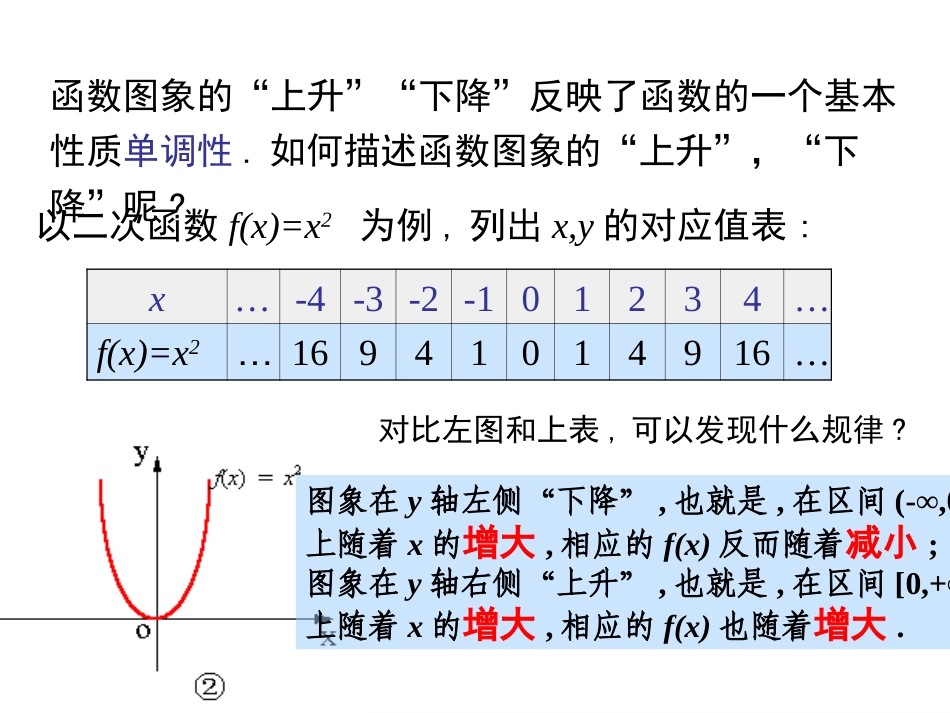
1.3函数的单调性1412108642-10-5510观察下列函数图象,体会它们的特点:函数图象的“上升”“下降”反映了函数的一个基本性质单调性.如何描述函数图象的“上升”,“下降”呢?x…-4-3-2-101234…f(x)=x2…16941014916…对比左图和上表,可以发现什么规律?图象在y轴左侧“下降”,也就是,在区间(-∞,0]上随着x的增大,相应的f(x)反而随着减小;图象在y轴右侧“上升”,也就是,在区间[0,+∞)上随着x的增大,相应的f(x)也随着增大.以二次函数f(x)=x2为例,列出x,y的对应值表:练习:利用刚才的方法描述一下左侧四个函数图象的“上升”“下降”的情况.22归纳探索、形成概念----探究规律理性认识22[0)?yx问题:如何从解析式的角度说明函数在,的图像上升函数xyO11234234512.xx任取两个自变量,;求差比较函数值的大小1x2xx…-4-3-2-101234…f(x)=x2…16941014916…22归纳探索、形成概念----探究规律理性认识1222121212121220,()()=()()0,()()()[0.xxfxfxxxxxxxfxfxfxx任意取有即所以在,)为增函数22[0)?yx问题:如何从解析式的角度说明函数在,的图像是上升的函数理性认识思考如何利用函数解析式f(x)=x2描述“随着x的增大,相应的f(x)反而随着减小.”“随着x的增大,相应的f(x)也随着增大.”?对于二次函数f(x)=x2,我们可以这样来描述:在区间(0,+∞)任意两个自变量的值x1,x2,得f(x1)=x12,f(x2)=x22,当x1<x2时,都有x12函数的单调性定义:如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)<f(x2),那么就说函数f(x)在区间D上是增函数如果对于定义域I内的某个区间D上的任意两个自变量的值x1,x2,当x1<x2时,都有f(x1)>f(x2),那么就说函数f(x)在区间D上是减函数注意比较这两句话的不同之处和共同之处.想一想为了说明一个函数在某个区间上是增函数还是减函数,我们应该重点说明哪些要素?xoyy=f(x)x1x2f(x2)f(x1)xoyx1x2f(x1)f(x2)y=f(x)1、函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;注意:2、必须是对于区间D内的任意两个自变量x1,x2;当x1f(x2)分别是增函数和减函数.(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)在单调区间上,增函数的图象是上升的,减函数的图象是下降的。判断:1)函数f(x)=x2在是单调增函数;,xyo2yx(3)x1,x2取值的任意性(1)在单调区间上,增函数的图象是上升的,减函数的图象是下降的。(2)函数单调性是针对某个区间而言的,是一个局部性质;yxO12f(1)f(2)判断:2)定义在R上的函数f(x)满足f(2)>f(1),则函数f(x)在[1,2]上是增函数;例1、下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?解:函数y=f...